题目内容
【题目】某创业团队拟生产![]() 两种产品,根据市场预测,
两种产品,根据市场预测, ![]() 产品的利润与投资额成正比(如图1),
产品的利润与投资额成正比(如图1),![]() 产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)
产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)

(1)分別将![]() 两种产品的利润
两种产品的利润![]() 、
、![]() 表示为投资额
表示为投资额![]() 的函数;
的函数;
(2)该团队已筹集到10 万元资金,并打算全部投入![]() 两种产品的生产,问:当
两种产品的生产,问:当![]() 产品的投资额为多少万元时,生产
产品的投资额为多少万元时,生产![]() 两种产品能获得最大利润,最大利润为多少?
两种产品能获得最大利润,最大利润为多少?
【答案】(1)![]() ,
, ![]() ;(2)6.25, 4.0625.
;(2)6.25, 4.0625.
【解析】试题分析:(1)由![]() 产品的利润与投资额成正比,
产品的利润与投资额成正比, ![]() 产品的利润与投资额的算术平方根成正比,结合函数图象,我们可以利用待定系数法来求两种产品的收益与投资的函数关系;(2)由(1)的结论,我们设
产品的利润与投资额的算术平方根成正比,结合函数图象,我们可以利用待定系数法来求两种产品的收益与投资的函数关系;(2)由(1)的结论,我们设![]() 产品的投资额为
产品的投资额为![]() 万元,则
万元,则![]() 产品的投资额为
产品的投资额为![]() 万元,这时可以构造出一个关于收益
万元,这时可以构造出一个关于收益![]() 的函数,然后利用求函数最大值的方法进行求解.
的函数,然后利用求函数最大值的方法进行求解.
试题解析:(1) ![]() ,
,
![]() .
.
(2) 设![]() 产品的投资额为
产品的投资额为![]() 万元,则
万元,则![]() 产品的投资额为
产品的投资额为![]() 万元,
万元,
创业团队获得的利润为![]() 万元,
万元,
则![]()
![]()
![]() ,
,
令![]() ,
, ![]() ,即
,即![]() ,
,
当![]() ,即
,即![]() 时,
时, ![]() 取得最大值4.0625.
取得最大值4.0625.
答:当![]() 产品的投资额为6.25万元时,创业团队获得的最大利润为4.0625 万元.
产品的投资额为6.25万元时,创业团队获得的最大利润为4.0625 万元.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如表对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)求广告费支出x与销售额y回归直线方程 ![]() =bx+a(a,b∈R);
=bx+a(a,b∈R);
已知b= 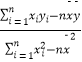 ,
, ![]()
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.