题目内容
 在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,
在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,(1)将四边形EFGH的面积S表示成x的函数,并写出函数的定义域;
(2)当x为何值时,四边形EFGH的面积最大?并求出最大面积.
分析:(1)分别求出矩形四个角落的三角形的面积,再利用矩形的面积减去四个角落的三角形的面积,可得四边形EFGH的面积S;
(2)先配方,确定函数的对称轴,再与函数的定义域结合,分类求出四边形EFGH的面积最大值.
(2)先配方,确定函数的对称轴,再与函数的定义域结合,分类求出四边形EFGH的面积最大值.
解答:解:(1)由题意,S△AHE=S△CGF=
x2,S△DGH=S△BEF=
(a-x)(b-x)
∴SEFGH=ab-2[
x2+
(a-x)(b-x)]=-2x2+(a+b)x(0<x≤b)…(5分)
(2)SEFGH=-2x2+(a+b)x=-2(x-
)2+
(0<x≤b)
若
≤b,即b<a≤3b时,当x=
时,Smax=
…(9分)
若
>b,即a>3b时,S(x)在(0,b]上为增函数,当x=b时,Smax=ab-b2…(12分)
| 1 |
| 2 |
| 1 |
| 2 |
∴SEFGH=ab-2[
| 1 |
| 2 |
| 1 |
| 2 |
(2)SEFGH=-2x2+(a+b)x=-2(x-
| a+b |
| 4 |
| (a+b)2 |
| 8 |
若
| a+b |
| 4 |
| a+b |
| 4 |
| (a+b)2 |
| 8 |
若
| a+b |
| 4 |
点评:本题重点考查四边形面积的计算,考查利用配方法求二次函数的最值,应注意函数的对称轴与区间结合,确定分类的标准.

练习册系列答案
相关题目
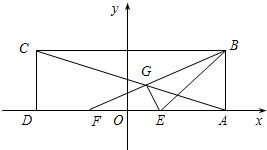 在矩形ABCD中,已知AD=6,AB=2,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H.以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系.
在矩形ABCD中,已知AD=6,AB=2,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H.以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系. 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: 在矩形ABCD中,已知AD=2AB=2,点E是AD得中点,将△DEC沿CE折起到△D′EC的位置,使平面D′EC⊥平面BEC.
在矩形ABCD中,已知AD=2AB=2,点E是AD得中点,将△DEC沿CE折起到△D′EC的位置,使平面D′EC⊥平面BEC. 如图,在矩形ABCD中,已知AB=3AD,E,F为AB的两个三等分点,AC,DF交于点G;
如图,在矩形ABCD中,已知AB=3AD,E,F为AB的两个三等分点,AC,DF交于点G;