题目内容
设a,b均为大于1的自然数,函数f(x)=a(b+sinx),g(x)=b+cosx,若存在实数m,使得f(m)=g(m),则a+b= .
【答案】分析:利用f(m)=g(m),推出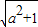 •sin(m-θ)=b(1-a),利用三角函数的有界性,推出a,b的关系,结合a,b均为大于1的自然数,讨论a,b的范围,求出a,b的值即可.
•sin(m-θ)=b(1-a),利用三角函数的有界性,推出a,b的关系,结合a,b均为大于1的自然数,讨论a,b的范围,求出a,b的值即可.
解答:解:由f(m)=g(m),
即a(b+sinm)=b+cosm
asinm-cosm=b-ab
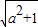 •sin(m-θ)=b(1-a)[注:sinθ=
•sin(m-θ)=b(1-a)[注:sinθ=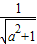 ]
]
∵-1≤sin(m-θ)≤1
∴-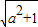 ≤b(1-a)≤
≤b(1-a)≤
∵a,b均为大于1的自然数
∴1-a<0 b(1-a)<0,
∴b(1-a)≥-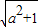 ,
,
b(a-1)≤
b≤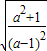 =
=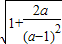 .
.
∵a≥4时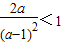 ,b<2
,b<2
∴a<4
当a=2时 b≤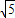 ,b=2
,b=2
当a=3时 b≤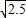 无解
无解
综上:a=2,b=2
a+b=4.
故答案为:4.
点评:本题考查三角函数的有界性,基本不等式的应用,考查计算能力,转化思想.
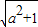 •sin(m-θ)=b(1-a),利用三角函数的有界性,推出a,b的关系,结合a,b均为大于1的自然数,讨论a,b的范围,求出a,b的值即可.
•sin(m-θ)=b(1-a),利用三角函数的有界性,推出a,b的关系,结合a,b均为大于1的自然数,讨论a,b的范围,求出a,b的值即可.解答:解:由f(m)=g(m),
即a(b+sinm)=b+cosm
asinm-cosm=b-ab
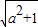 •sin(m-θ)=b(1-a)[注:sinθ=
•sin(m-θ)=b(1-a)[注:sinθ=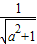 ]
]∵-1≤sin(m-θ)≤1
∴-
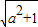 ≤b(1-a)≤
≤b(1-a)≤
∵a,b均为大于1的自然数
∴1-a<0 b(1-a)<0,
∴b(1-a)≥-
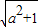 ,
,b(a-1)≤

b≤
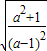 =
=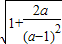 .
.∵a≥4时
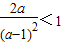 ,b<2
,b<2∴a<4
当a=2时 b≤
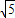 ,b=2
,b=2当a=3时 b≤
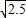 无解
无解综上:a=2,b=2
a+b=4.
故答案为:4.
点评:本题考查三角函数的有界性,基本不等式的应用,考查计算能力,转化思想.

练习册系列答案
相关题目