题目内容
已知函数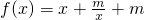 (x∈[1,+∞)且m<1).
(x∈[1,+∞)且m<1).
(Ⅰ)用定义证明函数f(x)在[1,+∞)上为增函数;
(Ⅱ)设函数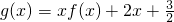 ,若[2,5]是g(x)的一个单调区间,且在该区间上g(x)>0恒成立,求实数m的取值范围.
,若[2,5]是g(x)的一个单调区间,且在该区间上g(x)>0恒成立,求实数m的取值范围.
(Ⅰ)证明:设1≤x1<x2<+∞,
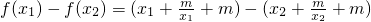 =(x1-x2)(
=(x1-x2)( )
)
∵1≤x1<x2<+∞,m<1,
∴x1-x2<0, >0,
>0,
∴f(x1)<f(x2)
∴函数f(x)在[1,+∞)上为增函数.
(Ⅱ)解: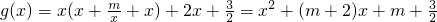
对称轴 ,定义域x∈[2,5]
,定义域x∈[2,5]
①g(x)在[2,5]上单调递增,且g(x)>0,
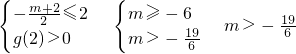
②g(x)在[2,5]上单调递减,且g(x)>0,
 无解
无解
综上所述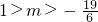
分析:(Ⅰ)设1≤x1<x2<+∞,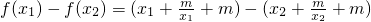 =(x1-x2)(
=(x1-x2)( ),由1≤x1<x2<+∞,m<1,能够证明函数f(x)在[1,+∞)上为增函数.
),由1≤x1<x2<+∞,m<1,能够证明函数f(x)在[1,+∞)上为增函数.
(Ⅱ)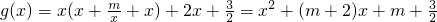 ,对称轴
,对称轴 ,定义域x∈[2,5],由此进行分类讨论,能够求出实数m的取值范围.
,定义域x∈[2,5],由此进行分类讨论,能够求出实数m的取值范围.
点评:本题考查函数的恒成立问题的性质和应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.解题时要认真审题,仔细解答.
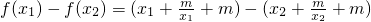 =(x1-x2)(
=(x1-x2)( )
)∵1≤x1<x2<+∞,m<1,
∴x1-x2<0,
 >0,
>0,∴f(x1)<f(x2)
∴函数f(x)在[1,+∞)上为增函数.
(Ⅱ)解:
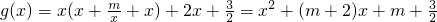
对称轴
 ,定义域x∈[2,5]
,定义域x∈[2,5]①g(x)在[2,5]上单调递增,且g(x)>0,
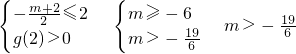
②g(x)在[2,5]上单调递减,且g(x)>0,
 无解
无解综上所述
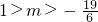
分析:(Ⅰ)设1≤x1<x2<+∞,
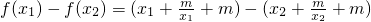 =(x1-x2)(
=(x1-x2)( ),由1≤x1<x2<+∞,m<1,能够证明函数f(x)在[1,+∞)上为增函数.
),由1≤x1<x2<+∞,m<1,能够证明函数f(x)在[1,+∞)上为增函数.(Ⅱ)
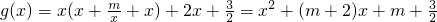 ,对称轴
,对称轴 ,定义域x∈[2,5],由此进行分类讨论,能够求出实数m的取值范围.
,定义域x∈[2,5],由此进行分类讨论,能够求出实数m的取值范围.点评:本题考查函数的恒成立问题的性质和应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.解题时要认真审题,仔细解答.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知函数g(x)=
,函数f(x)=x2?g(x),则满足不等式f(a-2)+f(a2)>0的实数a的取值范围是( )
|
| A、(-2,1) |
| B、(-1,2) |
| C、(-∞,-2)∪(1,+∞) |
| D、(-∞,-1)∪(2,+∞) |
