题目内容
已知函数 (
( R,
R, ,
, ,
, )图象如图,P是图象的最高点,Q为图象与
)图象如图,P是图象的最高点,Q为图象与 轴的交点,O为原点.且
轴的交点,O为原点.且 ,
, ,
, .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)将函数 图象向右平移1个单位后得到函数
图象向右平移1个单位后得到函数 的图象,当
的图象,当 时,求函数
时,求函数 的最大值.
的最大值.
(Ⅰ)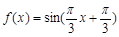 (Ⅱ)
(Ⅱ)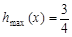 .
.
解析试题分析:(Ⅰ)由余弦定理得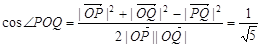 ,
,
∴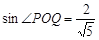 ,得P点坐标为
,得P点坐标为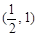 .
.
∴ 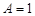 ,
,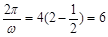 ,
,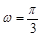 .
.
由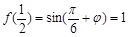 ,得
,得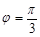 .
.
∴ 的解析式为
的解析式为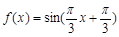
(Ⅱ) ,
, 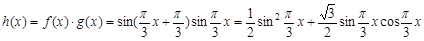
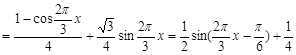 .
.
当 时,
时, ,
,
∴ 当 ,即
,即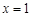 时
时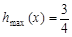 .
.
考点:余弦定理,正弦型函数解析式,函数平移,二倍角公式。
点评:本题考查正确运用余弦定理和二倍角公式运算化简。

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
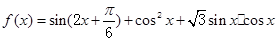 .
.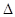 ABC的三个内角,若cosB=
ABC的三个内角,若cosB=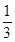 ,
,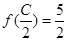 ,求sinA.
,求sinA.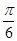 )+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
)+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为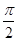 .
.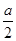 )=2,求α的值.
)=2,求α的值.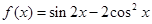
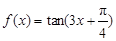
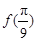 的值;
的值;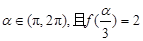 ,求
,求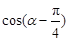 的值.
的值.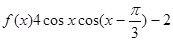
 上的最大值和最小值.
上的最大值和最小值.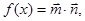 设
设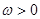 ,
, 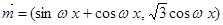 ,
,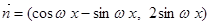 ,若
,若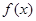 图象中相邻的两条对称轴间的距离等于
图象中相邻的两条对称轴间的距离等于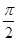 .
.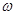 的值;
的值;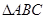 中,
中,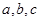 分别为角
分别为角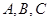 的对边,
的对边,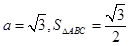 .当
.当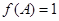 时,求
时,求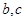 的值.
的值.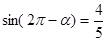 ,
,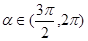 ,求
,求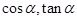 ;
;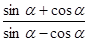 的值。
的值。