题目内容
已知双曲线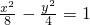 的左焦点为F,△ABC的三个顶点均在其左支上,若
的左焦点为F,△ABC的三个顶点均在其左支上,若 ,则|
,则| |+|
|+|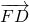 |+|
|+|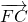 |=________.
|=________.
2
分析:求出焦点坐标和左准线方程,根据F 为△ABC的重心,可得x1+x2+x3=-6 ,由双曲线的第二定义可得
,由双曲线的第二定义可得
| |+|
|+|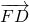 |+|
|+|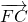 |=e[(
|=e[( )+(
)+( )+(
)+( )],由此求得结果.
)],由此求得结果.
解答:由题意可得 F(-2 ,0),左准线为 x=-
,0),左准线为 x=- ,e=
,e= ,设△ABC的三个顶点的坐标分别为
,设△ABC的三个顶点的坐标分别为
(x1,y1),(x2,y2),(x3,y3 ).∵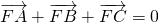 ,∴F 为△ABC的重心,
,∴F 为△ABC的重心,
∴ ,∴x1+x2+x3=-6
,∴x1+x2+x3=-6 ,由双曲线的第二定义可得
,由双曲线的第二定义可得
| |+|
|+|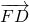 |+|
|+|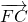 |=e[(
|=e[( )+(
)+( )+(
)+( )]=
)]= [-
[- -(x1+x2+x3)]
-(x1+x2+x3)]
=2 ,
,
故答案为:2 .
.
点评:本题考查双曲线的定义和标准方程,以及双曲线的简单性质的应用,得到| |+|
|+|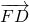 |+|
|+|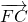 |=
|=
e[( )+(
)+( )+(
)+( )],是解题的关键.
)],是解题的关键.

分析:求出焦点坐标和左准线方程,根据F 为△ABC的重心,可得x1+x2+x3=-6
 ,由双曲线的第二定义可得
,由双曲线的第二定义可得|
 |+|
|+|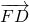 |+|
|+|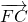 |=e[(
|=e[( )+(
)+( )+(
)+( )],由此求得结果.
)],由此求得结果.解答:由题意可得 F(-2
 ,0),左准线为 x=-
,0),左准线为 x=- ,e=
,e= ,设△ABC的三个顶点的坐标分别为
,设△ABC的三个顶点的坐标分别为(x1,y1),(x2,y2),(x3,y3 ).∵
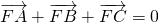 ,∴F 为△ABC的重心,
,∴F 为△ABC的重心,∴
 ,∴x1+x2+x3=-6
,∴x1+x2+x3=-6 ,由双曲线的第二定义可得
,由双曲线的第二定义可得 |
 |+|
|+|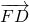 |+|
|+|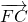 |=e[(
|=e[( )+(
)+( )+(
)+( )]=
)]= [-
[- -(x1+x2+x3)]
-(x1+x2+x3)]=2
 ,
,故答案为:2
 .
.点评:本题考查双曲线的定义和标准方程,以及双曲线的简单性质的应用,得到|
 |+|
|+|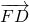 |+|
|+|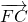 |=
|=e[(
 )+(
)+( )+(
)+( )],是解题的关键.
)],是解题的关键. 
练习册系列答案
相关题目
 的左焦点为F1,左、右顶点分别为A1、A2,P为双曲线上任意一点,则分别以线段PF1,A1A2为直径的两个圆的位置关系为( )
的左焦点为F1,左、右顶点分别为A1、A2,P为双曲线上任意一点,则分别以线段PF1,A1A2为直径的两个圆的位置关系为( ) 的左焦点为
的左焦点为 ,点
,点 为双曲线右支上一点,且
为双曲线右支上一点,且 与圆
与圆 相切于点
相切于点 ,
, 为线段
为线段 为坐标原点, 则
为坐标原点, 则 =
=  的左焦点为
的左焦点为 ,
, ,当
,当 时,则该双曲线的离心率
时,则该双曲线的离心率 等于 ( )
等于 ( )
 B.
B.
 C.
C.
 D
.
D
. 
 的左焦点为
的左焦点为 ,点
,点 为双曲线右支上一点,且
为双曲线右支上一点,且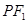 与圆
与圆 相切于点
相切于点 ,
, 为线段
为线段 为坐标原点,则
为坐标原点,则 =
=