题目内容
1.已知数列{an}满足:a1=$\frac{1}{2}$,$\frac{3(1+{a}_{n+1})}{1-{a}_{n}}$=$\frac{2(1+{a}_{n})}{1-{a}_{n+1}}$,anan+1<0(n≥1);数列{bn}满足:bn=a${\;}_{n+1}^{2}$-a${\;}_{n}^{2}$(n≥1).(1)求数列{an},{bn}的通项公式;
(2)求数列{4(n+1)bn}的前n项和Tn.
分析 (1)把已知数列递推式变形,可得数列{$1-{{a}_{n}}^{2}$}是1-$\frac{1}{4}=\frac{3}{4}$为首项,以$\frac{2}{3}$为公比的等比数列,求其通项公式后结合anan+1<0可得数列{an}的通项公式,代入${b}_{n}={{a}_{n+1}}^{2}-{{a}_{n}}^{2}$可得数列{bn}的通项公式;
(2)把数列{bn}的通项公式代入数列{4(n+1)bn},由错位相减法求得其前n项和Tn.
解答 解:(1)∵$\frac{3(1+{a}_{n+1})}{1-{a}_{n}}$=$\frac{2(1+{a}_{n})}{1-{a}_{n+1}}$,
∴$\frac{1-{{a}_{n+1}}^{2}}{1-{{a}_{n}}^{2}}=\frac{2}{3}$,
∴数列{$1-{{a}_{n}}^{2}$}是1-$\frac{1}{4}=\frac{3}{4}$为首项,以$\frac{2}{3}$为公比的等比数列,
∴$1-{{a}_{n}}^{2}=\frac{3}{4}•(\frac{2}{3})^{n-1}$.
∴${{a}_{n}}^{2}=1-\frac{3}{4}•(\frac{2}{3})^{n-1}$.
∵anan+1<0,
∴${a}_{n}=(-1)^{n+1}\sqrt{1-\frac{3}{4}•(\frac{2}{3})^{n-1}}$;
${b}_{n}={{a}_{n+1}}^{2}-{{a}_{n}}^{2}$=$[1-\frac{3}{4}•(\frac{2}{3})^{n}]-[1-\frac{3}{4}•(\frac{2}{3})^{n-1}]=\frac{1}{4}•(\frac{2}{3})^{n-1}$;
(2)∵4(n+1)bn=$(n+1)•(\frac{2}{3})^{n-1}$.
∴${T}_{n}=2•(\frac{2}{3})^{0}+3•(\frac{2}{3})^{1}+4•(\frac{2}{3})^{2}+…+n•(\frac{2}{3})^{n-2}$$+(n+1)•(\frac{2}{3})^{n-1}$.
$\frac{2}{3}{T}_{n}=2•(\frac{2}{3})^{1}+3•(\frac{2}{3})^{2}+…+n•(\frac{2}{3})^{n-1}+(n+1)•(\frac{2}{3})^{n}$.
两式作差可得$\frac{1}{3}{T}_{n}=2+\frac{2}{3}+(\frac{2}{3})^{2}+(\frac{2}{3})^{3}+…+(\frac{2}{3})^{n-1}-(n+1)•(\frac{2}{3})^{n}$
=2+$\frac{\frac{2}{3}[1-(\frac{2}{3})^{n-1}]}{1-\frac{2}{3}}-(n+1)•(\frac{2}{3})^{n}$=4-(n+4)•$(\frac{2}{3})^{n}$.
∴${T}_{n}=12-(3n+12)•(\frac{2}{3})^{n}$.
点评 本题考查数列递推式,考查了等比关系的确定,训练了错位相减法求数列的前n项和,是中档题.

| A. | (-$\sqrt{e}$,$\sqrt{e}$) | B. | (-$\sqrt{e}$,+∞) | C. | (-∞,$\sqrt{e}$) | D. | ($\sqrt{e}$,+∞) |
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
 在三棱锥P-ABC中,PA、PB、PC两两垂直,AC=BC=2PA=2PB=4,E、F分别是AC、BC的中点.
在三棱锥P-ABC中,PA、PB、PC两两垂直,AC=BC=2PA=2PB=4,E、F分别是AC、BC的中点.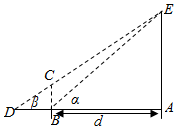 为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木AE的高度H(m),垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β(D,C,E三点共线),试根据上述测量方案,回答如下问题:
为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木AE的高度H(m),垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β(D,C,E三点共线),试根据上述测量方案,回答如下问题: 如图,用四中不同的颜色给图中的A、B、C、D、E涂色,要求每个点涂一种颜色,且图中每条线段的两端点涂不同颜色,则不同的涂色方法有144种.
如图,用四中不同的颜色给图中的A、B、C、D、E涂色,要求每个点涂一种颜色,且图中每条线段的两端点涂不同颜色,则不同的涂色方法有144种.