题目内容
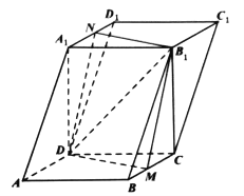
【题目】如图,在四棱柱![]() 中,底面
中,底面![]() 是正方形,平面
是正方形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .过顶点
.过顶点![]() ,
,![]() 的平面与棱
的平面与棱![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:四边形![]() 是平行四边形;
是平行四边形;
(Ⅲ)若![]() ,试判断二面角
,试判断二面角![]() 的大小能否为
的大小能否为![]() ?说明理由.
?说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)不能为![]() .
.
【解析】
(1)由平面![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,从而证明
,从而证明![]() ;
;
(2)由平面![]() 与平面
与平面![]() 没有交点,可得
没有交点,可得![]() 与
与![]() 不相交,又
不相交,又![]() 与
与![]() 共面,所以
共面,所以![]()
![]() ,同理可证
,同理可证![]()
![]() ,得证;(3)作
,得证;(3)作![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,根据三垂线定理,确定二面角
,根据三垂线定理,确定二面角![]() 的平面角
的平面角![]() ,若
,若![]() ,
,![]() ,由大角对大边知
,由大角对大边知![]() ,两者矛盾,故二面角
,两者矛盾,故二面角![]() 的大小不能为
的大小不能为![]() .
.
(1)由平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
且![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ;
;
(2)依题意![]() 都在平面
都在平面![]() 上,
上,
因此![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
平面![]() 与平面
与平面![]() 平行,即两个平面没有交点,
平行,即两个平面没有交点,
则![]() 与
与![]() 不相交,又
不相交,又![]() 与
与![]() 共面,
共面,
所以![]()
![]() ,同理可证
,同理可证![]()
![]() ,
,
所以四边形![]() 是平行四边形;
是平行四边形;
(3)不能.如图,作![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
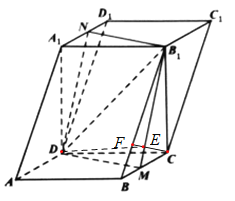
由![]() ,
,![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() ,又
,又![]() ,
,
根据三垂线定理,得到![]() ,所以
,所以![]() 是二面角
是二面角![]() 的平面角,
的平面角,
若![]() ,则
,则![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
又![]() ,
,
所以![]() 中,由大角对大边知
中,由大角对大边知![]() ,
,
所以![]() ,这与上面
,这与上面![]() 相矛盾,
相矛盾,
所以二面角![]() 的大小不能为
的大小不能为![]() .
.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】某学校为了调查学生数学素养的情况,从初中部、高中部各随机抽取100名学生进行测试.初中部的100名学生的成绩(单位:分)的频率分布直方图如图所示.
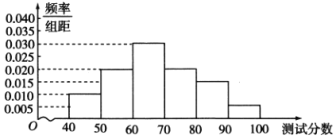
高中部的100名学生的成绩(单位:分)的频数分布表如下:
测试分数 |
|
|
|
|
|
频数 | 5 | 20 | 35 | 25 | 15 |
把成绩分为四个等级:60分以下为![]() 级,60分(含60)到80分为
级,60分(含60)到80分为![]() 级,80分(含80)到90分为
级,80分(含80)到90分为![]() 级,90分(含90)以上为
级,90分(含90)以上为![]() 级.
级.
(1)根据已知条件完成下面的![]() 列联表,据此资料你是否有99%的把握认为学生数学素养成绩“
列联表,据此资料你是否有99%的把握认为学生数学素养成绩“![]() 级”与“所在级部”有关?
级”与“所在级部”有关?
不是 |
| 合计 | |
初中部 | |||
高中部 | |||
合计 |
注: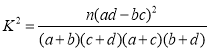 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(2)若这个学校共有9000名高中生,用频率估计概率,用样本估计总体,试估计这个学校的高中生的数学素养成绩为![]() 级的人数,并估计数学素养成绩的平均分(用组中值代表本组分数);
级的人数,并估计数学素养成绩的平均分(用组中值代表本组分数);
(3)把初中部的![]() 级同学编号为
级同学编号为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,高中部的
,高中部的![]() 级同学编号为
级同学编号为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,从初中部
,从初中部![]() 级、高中部
级、高中部![]() 级中各选一名同学,求这两名同学的编号奇偶性相同的概率.
级中各选一名同学,求这两名同学的编号奇偶性相同的概率.
【题目】已知![]() 为等差数列,
为等差数列,![]() ,
,![]() ,
,![]() 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且![]() ,
,![]() ,
,![]() 中的任何两个数都不在下表的同一列.
中的任何两个数都不在下表的同一列.
第一列 | 第二列 | 第三列 | |
第一行 | |||
第二行 | 4 | 6 | 9 |
第三行 | 12 | 8 | 7 |
请从①![]() ,②
,②![]() ,③
,③ ![]() 的三个条件中选一个填入上表,使满足以上条件的数列
的三个条件中选一个填入上表,使满足以上条件的数列![]() 存在;并在此存在的数列
存在;并在此存在的数列![]() 中,试解答下列两个问题
中,试解答下列两个问题
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.