题目内容

14．已知-圆柱形圆木，高10米，底面半径R米，把圆木锯成高10米的长方体形柱木，问柱木底面的长和宽分别为多少米时，其体积最大．

分析 求解体积是最大值，利用转化思想，就是求解底面矩形面积的最大值，设出长与宽列出关系式求解即可．

解答 解：圆柱形圆木，高10米，底面半径R米，把圆木锯成高10米的长方体形柱木，柱木体积最大时，就是圆柱底面矩形的面积最大值，
设矩形的长为：x，则宽为y，由题意可得x2+y2=4R2．
矩形的面积为：S=xy≤$\frac{{x}^{2}+{y}^{2}}{2}$=2R2．当且仅当x=y=$\sqrt{2}$R时，底面矩形面积最大，此时高10米的长方体形柱木的体积最大．

点评 本题考查几何体的体积的最值的求法，基本不等式的应用，考查计算能力以及转化思想的应用．

练习册系列答案
相关题目
4．已知函数f（x）=ex-mxk（m，k∈R）定义域为（0，+∞）
（Ⅰ）若k=1时，f（x）在（1，+∞）上有最小值，求m的取值范围；
（Ⅱ）若k=2时，f（x）的值域为[0，+∞），试求m的值；
（Ⅲ）试证：对任意实数m，k，总存在x0，使得当x∈（x0，+∞）时，恒有f（x）＞0．
5．已知抛物线y2=4x，点A（1，2），过点A任意作两条倾斜角互补的直线，分别于抛物线交于两点P，Q．证明：直线PQ的斜率为定值．
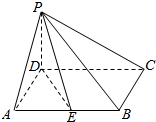2．已知四棱锥P-ABCD，底面ABCD是菱形，∠DAB=60°，PD⊥平面ABCD，点E为AB中点．
证明：平面PED⊥平面PAB．
9．已知抛物线y=ax2和直线1：x+y-1=0，若抛物线上总存在关于l对称的两点，求实数a的取值范围．
19．已知直线11：ax-y+1=0与l2：x+ay+1=0（a∈R）．
（1）判定两直线的位置关系；
（2）求11与12的交点C的轨迹方程和其面积S的值．
6．当x∈[-2，2]时，函数f（x）=|x5-5x|的最大值为22．
12．已知四面体ABCD，下列命题：
①若AB⊥CD，则AC⊥BD；
②若AC=BC=AD=BD，则AB⊥CD；
③若点E，F分别在BC，BD上，且CD∥平面AEF，则EF是△BCD的中位线；
④若E是CD中点，则CD⊥平面ABE；
⑤在棱AB上任取一点P，使三棱锥P-BCD的体积与四面体ABCD的体积比大于$\frac{1}{3}$的概率为$\frac{2}{3}$．
其中正确的命题的序号是②⑤（填写所有真命题序号）
13．设F1、F2分别是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，P是C的右支上的点，射线PT平分∠F1PF2，过原点O做PT的平行线交PF1于点M，若|MP|=$\frac{1}{3}$|F1F2|，则C的离心率为$\frac{3}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网