题目内容
设函数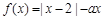 .
.
(Ⅰ)当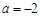 时,解不等式
时,解不等式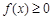 ;
;
(Ⅱ)当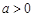 时,不等式
时,不等式 的解集为
的解集为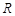 ,求实数
,求实数 的取值范围.
的取值范围.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)原不等式的解集等价于不等式组 或
或 的解集的并集;(Ⅱ)当
的解集的并集;(Ⅱ)当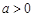 时,不等式
时,不等式 的解集为
的解集为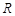 ,恒成立问题,对
,恒成立问题,对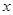 分类讨论,①
分类讨论,① ,②
,② .
.
试题解析:(Ⅰ)当 时,
时, ,
,

 或
或

 或
或 ,
,
∴不等式 的解集是
的解集是 . 5分
. 5分
(Ⅱ)不等式 可化为
可化为 ,
,
∴ ,
,
由题意, 时
时 恒成立,
恒成立,
当 时,
时, 可化为
可化为 ,
, ,
, ,
, ,
,
综上,实数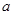 的取值范围是
的取值范围是 . 10分
. 10分
考点:绝对值不等式,恒成立问题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
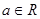 ,解关于
,解关于 的不等式
的不等式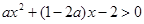 .
.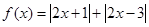 .
. 的不等式
的不等式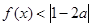 的解集不是空集,求实数
的解集不是空集,求实数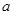 的取值范围;
的取值范围;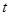 的一元二次方程
的一元二次方程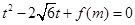 有实根,求实数
有实根,求实数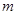 的取值范围.
的取值范围. 的不等式
的不等式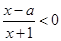 的解集为
的解集为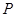 ,不等式
,不等式 的解集为
的解集为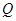 .
.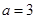 ,求
,求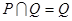 ,求正数
,求正数 的取值.
的取值. 是定义在
是定义在 上的偶函数,
上的偶函数, ,当
,当 时,
时, .
. ;
;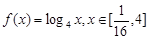 的值域为集合
的值域为集合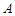 ,关于
,关于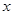 的不等式
的不等式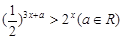 的解集为
的解集为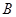 ,集合
,集合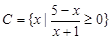 ,集合
,集合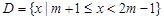
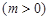
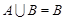 ,求实数
,求实数 的取值范围;
的取值范围;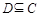 ,求实数
,求实数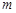 的取值范围。
的取值范围。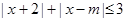 的解集为
的解集为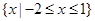 .
. 的值;
的值;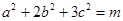 ,求
,求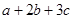 的取值范围.
的取值范围.
 ,集合B=
,集合B= 。
。 =2时,求
=2时,求 ;
; 时,求使
时,求使 的实数
的实数