题目内容
已知x∈R设f（x）是奇函数，g（x）是偶函数并且f（x）-g（x）=x2-x3
（1）求f（x）的解析式；
（2）判断f（x）的单调性并用定义证明．
（1）求f（x）的解析式；
（2）判断f（x）的单调性并用定义证明．
分析：（1）根据f（x）-g（x）=x2-x3 ①，f（x）是奇函数，g（x）是偶函数，可得f（-x）-g（-x）=-f（x）-g（x）=x2+x3 ②．由①、②解得f（x）的解析式．
（2）设x1＜x2，化简 f（x1）-f（x2）为 （x1-x2）（[(x1+
)2+
]，小于零，可得 f（x1）＜f（x2），函数f（x）是R上的减函数．
（2）设x1＜x2，化简 f（x1）-f（x2）为 （x1-x2）（[(x1+
| x2 |
| 2 |
| 3x22 |
| 4 |
解答：解：（1）∵f（x）-g（x）=x2-x3 ①，因为f（x）是奇函数，g（x）是偶函数，
所以，f（-x）-g（-x）=-f（x）-g（x）=x2+x3 ②．
由①、②解得f（x）=-x3．
（2）f（x）是单调减函数．
证明：设x1＜x2，则 f（x1）-f（x2）=-x13-（-x23 ）=-（x1-x2）（x12+x1•x2+x22 ）=-（x1-x2）（[(x1+
)2+
]，
再由题设可得，（x1-x2）＜0，（[(x1+
)2+
]＞0，∴-（x1-x2）（[(x1+
)2+
]＞0，
即 f（x1）＞f（x2），故函数f（x）在R上是减函数．
所以，f（-x）-g（-x）=-f（x）-g（x）=x2+x3 ②．
由①、②解得f（x）=-x3．
（2）f（x）是单调减函数．
证明：设x1＜x2，则 f（x1）-f（x2）=-x13-（-x23 ）=-（x1-x2）（x12+x1•x2+x22 ）=-（x1-x2）（[(x1+
| x2 |
| 2 |
| 3x22 |
| 4 |
再由题设可得，（x1-x2）＜0，（[(x1+
| x2 |
| 2 |
| 3x22 |
| 4 |
| x2 |
| 2 |
| 3x22 |
| 4 |
即 f（x1）＞f（x2），故函数f（x）在R上是减函数．
点评：本题主要考查函数的奇偶性的应用，求函数的解析式，函数的单调性的判断和证明，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
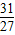，试求y=f（x）的解析式；
，
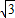]且a为常数，求θ的取值范围．