题目内容
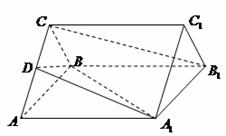
如图,正三棱柱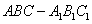 的底面边长是
的底面边长是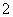 ,侧棱长是
,侧棱长是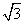 ,
,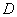 是
是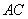 的中点.
的中点.
(1)求证: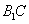 ∥平面
∥平面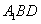 ;
;
(2)求二面角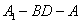 的大小;
的大小;
(3)在线段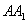 上是否存在一点
上是否存在一点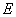 ,使得平面
,使得平面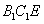
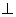 平面
平面 ,若存在,求出
,若存在,求出 的长;若不存在,说明理由.
的长;若不存在,说明理由.
(1)证明:连结 交
交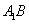 于
于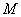 ,连结
,连结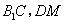 ,因为三棱柱
,因为三棱柱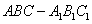 是正三棱柱,
是正三棱柱,
所以四边形 是矩形,所以
是矩形,所以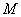 为
为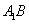 的中点.因为
的中点.因为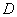 是
是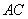 的中点,所以
的中点,所以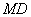 是三角形
是三角形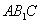 的中位线,所以
的中位线,所以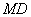 ∥
∥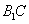 . 因为
. 因为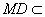 平面
平面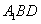 ,
,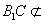 平面
平面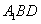 ,所以
,所以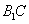 ∥平面
∥平面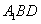 .
.
(2)解:作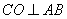 于
于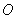 ,所以
,所以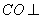 平面
平面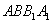 ,所以在正三棱柱
,所以在正三棱柱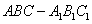 中如图建立空间直角坐标系
中如图建立空间直角坐标系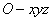 .因为
.因为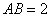 ,
,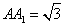 ,
,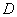 是
是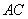 的中点.所以
的中点.所以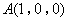 ,
,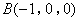 ,
, ,
,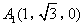 ,所以
,所以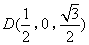 ,
, ,
,
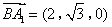 .设
.设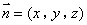 是平面
是平面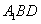 的法向量,所以
的法向量,所以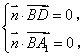 即
即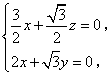 令
令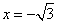 ,则
,则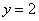 ,
, ,所以
,所以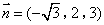 是平面
是平面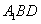 的一个法向量.由题意可知
的一个法向量.由题意可知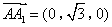 是平面
是平面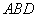 的一个法向量, 所以
的一个法向量, 所以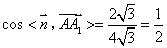 . 所以二面角
. 所以二面角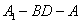 的大小为
的大小为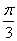 .
.
(3)设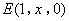 ,则
,则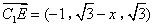 ,
,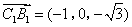 设平面
设平面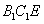 的法向量
的法向量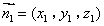 ,所以
,所以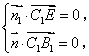 即
即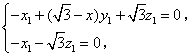
令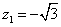 ,则
,则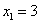 ,
,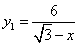 ,
, 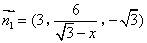 ,又
,又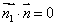 ,即
,即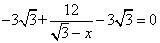 ,解得
,解得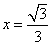 ,所以存在点
,所以存在点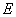 ,使得平面
,使得平面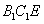
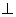 平面
平面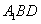 且
且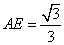 .
.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
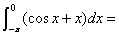 .
. 的两条直线分别切函数
的两条直线分别切函数 的图象于
的图象于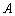 ,
, 两点.若直线
两点.若直线 的方程为
的方程为 ,则
,则 的值为( )
的值为( )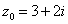 ,复数
,复数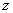 满足
满足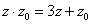 ,则复数
,则复数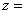 。
。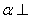 平面
平面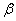 ,那么平面
,那么平面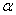 内一定存在直线平行于平面
内一定存在直线平行于平面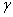 ,平面
,平面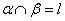 ,那么
,那么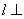 平面
平面 的棱长为
的棱长为 ,
, 、
、 分别是边
分别是边 、
、 上的中点,点
上的中点,点 是
是 上的动点,过点
上的动点,过点 交于点
交于点 ,设
,设 ,平行四边形
,平行四边形 的面积为
的面积为 ,设
,设 ,则
,则 关于
关于 的函数
的函数 的图像大致是 ( ).
的图像大致是 ( ).
 满足
满足 (
( ),则称数列
),则称数列 的公差为
的公差为 ,
, ,且数列
,且数列 是凹数列,则
是凹数列,则