题目内容
如图,棱长为1的正方体ABCD—A1B1C1D1中,P为DD1中点,O1、O2、O3分别是面A1C1、面BC1、面AC的中心.
(1)求证:B1O3⊥PA;
(2)求异面直线PO3与O1O2所成角的余弦值;
(3)求PO2的长.
(1)证明:以D为坐标原点,DA、DB、DD1所在直线为x轴、y轴、z轴建立如图所示空间直角坐标系D—xyz,

则A(1,0,0)、B1(1,1,1)、P(0,0,![]() )、O3(
)、O3(![]() ,
,![]() ,0),
,0),
∴![]() =(-
=(-![]() ,-
,-![]() ,-1),
,-1),![]() =(1,0,-
=(1,0,-![]() ).?
).?
∴![]() ·
·![]() =-
=-![]() ×1-
×1-![]() ×0-1×(-
×0-1×(-![]() )=0.?
)=0.?
∴v⊥![]() .∴B1O3⊥PA.?
.∴B1O3⊥PA.?
(2)解析:∵O1(![]() ,
,![]() ,1),O2(
,1),O2(![]() ,1,
,1,![]() ),?
),?
∴![]() =(0,
=(0,![]() ,-
,-![]() ).
).
又![]() =(
=(![]() ,
,![]() ,-
,-![]() ),设
),设![]() 与
与![]() 夹角为θ,
夹角为θ,
∴cosθ=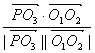 =
=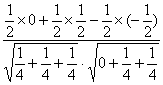 =
= =
=![]() .
.
∴异面直线PO3与O1O2所成角的余弦值为![]() .
.
(3)解析:∵P(0,0,![]() ),O2(
),O2(![]() ,1,
,1,![]() ),
),
∴|![]() |=
|=![]() ,故PO2的长为
,故PO2的长为![]() .
.

练习册系列答案
相关题目
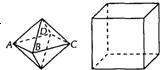


 两个相同的正四棱锥组成如图所示的几何体,可放入棱长为
两个相同的正四棱锥组成如图所示的几何体,可放入棱长为