题目内容
已知 为奇函数,当
为奇函数,当 时,
时, ;当
;当 时,
时, ,
,
若关于 的不等式
的不等式 有解,则
有解,则 的取值范围为_________.
的取值范围为_________.
 .
.
解析试题分析:显然 ,
, 可视为将函数
可视为将函数 的图象向左或向右平移
的图象向左或向右平移 个单位后所形成的,将
个单位后所形成的,将 的图象作出如下图所示,若
的图象作出如下图所示,若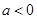 :则不等式
:则不等式 有解等价于将函数
有解等价于将函数 的图象向右平移
的图象向右平移 个单位后所得的函数
个单位后所得的函数 的图象存在位于函数
的图象存在位于函数 的图象上方的部分,由图可知
的图象上方的部分,由图可知 ,即
,即 ,若
,若 :同理可知,不等式
:同理可知,不等式 有解等价于将函数
有解等价于将函数 的图象向左平移
的图象向左平移 个单位后所得的函数
个单位后所得的函数 的图象存在位于函数
的图象存在位于函数 的图象上方的部分,由图可知,这是显然成立的,∴实数
的图象上方的部分,由图可知,这是显然成立的,∴实数 的取值范围是
的取值范围是 .
.
考点:1.奇函数的性质;2.函数与不等式相结合.

练习册系列答案
相关题目
各项不为零的等差数列 中,
中, ,数列
,数列 是等比数列,且
是等比数列,且 ,则
,则 ( )
( )
| A.2 | B.4 | C.8 | D.16 |
若 ,则下列不等式中,正确的不等式有 ( )
,则下列不等式中,正确的不等式有 ( )
① ②
② ③
③ ④
④
| A.1个 | B.2个 | C.3个 | D.4个 |
已知 ,则下列结论错误的是( )
,则下列结论错误的是( )
A. | B. | C. | D. |
不等式 的解集为
的解集为 ,则
,则 =( )
=( )
| A.10 | B.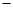 10 10 | C.14 | D.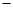 14 14 |
点 为不等式组
为不等式组 ,表示的平面区域上的一点,则
,表示的平面区域上的一点,则 的取值范围为
的取值范围为
A. | B. | C. | D. |
下列说法正确的是( )
| A.三点确定一个平面 |
| B.四边形一定是平面图形 |
| C.梯形一定是平面图形 |
D.平面 和平面 和平面 有不同在一条直线上的三个交点[来 有不同在一条直线上的三个交点[来 |
如果直线 、
、 与平面
与平面 、
、 、
、 满足:
满足: ,
, ∥
∥ ,
, 和
和 ,那么必有( )
,那么必有( )
A. ∥ ∥ 且 且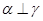 |
B.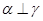 且 且 |
C. ∥ ∥ 且 且 |
D.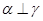 且 且 ∥ ∥ |
 满足
满足 ,则
,则 的最大值是_________.
的最大值是_________.