题目内容
1.已知函数f(x)=sin(ωx+$\frac{π}{3}$)(ω>0),A、B是函数y=f(x)图象上相邻的最高点和最低点,若|AB|=2$\sqrt{2}$,则f(1)=$\frac{\sqrt{3}}{2}$.分析 由图象上的两个相邻的最高点和最低点的距离为2$\sqrt{2}$求出ω,可得函数的解析式,即可求出f(1).
解答 解:由题意可得$\sqrt{4+\frac{{π}^{2}}{{ω}^{2}}}$=2$\sqrt{2}$,∴ω=$\frac{π}{2}$,
∴函数f(x)=sin($\frac{π}{2}$x+$\frac{π}{3}$),
∴f(1)=$\frac{\sqrt{3}}{2}$,
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,由图象上的两个相邻的最高点和最低点的距离为2$\sqrt{2}$求出ω是关键,属于中档题.

练习册系列答案
相关题目
6.某小组有男生8人,女生3人,从中随机抽取男生1人,女生2人,则男生甲和女生乙都被抽到的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{24}$ |
11.已知全集为R,集合A={x|x2-2x<3},B={x|x>2},则A∩(∁RB)( )
| A. | {x|-1<x<2} | B. | {x|2<x<3} | C. | {x|x<3} | D. | {x|-1<x≤2} |
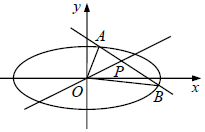 已知点P(t,$\frac{1}{2}$)在椭圆C:$\frac{{x}^{2}}{2}$+y2=1内,过P的直线l与椭圆C相交于A,B两点,且点P是线段AB的中点,O为坐标原点.
已知点P(t,$\frac{1}{2}$)在椭圆C:$\frac{{x}^{2}}{2}$+y2=1内,过P的直线l与椭圆C相交于A,B两点,且点P是线段AB的中点,O为坐标原点.