题目内容
10.已知sinα=-$\frac{1}{3}$,求tanα.分析 由sinα的值,利用同角三角函数间基本关系求出cosα的值,即可确定出tanα的值.
解答 解:∵sinα=-$\frac{1}{3}$,
∴cosα=±$\sqrt{1-si{n}^{2}α}$=±$\frac{2\sqrt{2}}{3}$,
则tanα=-$\frac{\sqrt{2}}{4}$或$\frac{\sqrt{2}}{4}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
20. 如图梯形ABCD中,AD∥BC,对角线AC、BD交于点O,点M,N分别在两腰上,MN过点O,且MN∥AD,OM=ON,则AD,BC,MN满足的关系是( )
如图梯形ABCD中,AD∥BC,对角线AC、BD交于点O,点M,N分别在两腰上,MN过点O,且MN∥AD,OM=ON,则AD,BC,MN满足的关系是( )
 如图梯形ABCD中,AD∥BC,对角线AC、BD交于点O,点M,N分别在两腰上,MN过点O,且MN∥AD,OM=ON,则AD,BC,MN满足的关系是( )
如图梯形ABCD中,AD∥BC,对角线AC、BD交于点O,点M,N分别在两腰上,MN过点O,且MN∥AD,OM=ON,则AD,BC,MN满足的关系是( )| A. | AD+BC=2MN | B. | AD•BC=MN2 | C. | $\frac{1}{AD}$+$\frac{1}{BC}$=$\frac{2}{MN}$ | D. | MN=$\sqrt{\frac{A{D}^{2}+B{C}^{2}}{2}}$ |
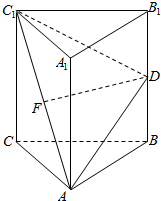 如图所示,棱柱ABC-A1B1C1为正三棱柱,且AC=C1C,其中点F,D分别为AC1,B1B的中点.
如图所示,棱柱ABC-A1B1C1为正三棱柱,且AC=C1C,其中点F,D分别为AC1,B1B的中点.