Question

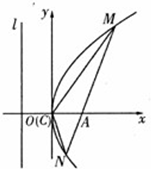如图，某旅游区拟在公路l（南北向）旁开发一个抛物线形的人工湖，湖沿岸上每一点到公路l的距离与到A处的距离相等，并在湖中建造一个三角形的游乐区MNC，三个顶点M，N，C都在湖沿岸上，直线通道MN经过A处．经测算，A在公路l正东方向200米处，C在A的正西方向100米处，现以点C为坐标原点，以线段CA所在直线为x轴建立平面直角坐标系．
（1）求抛物线的方程；
（2）试确定直线通道MN的位置，使得三角形游乐区MNC的面积最小，并求出最小值．

Answer 1

分析：（1）由题意，可得抛物线的焦点A（100，0），从而可求p，进而可求抛物线方程
（2）设点M（x₁，y₁），N（x₂，y₂）直线MN的方程为x=ny+100，联立直线与抛物线方程，根据方程根与系数关系，可得y₁+y₂，y₁y₂，代入|y₁-y₂|=

(y1+y2)2-4y1y2

，从而可S_△CMN=

1

2

|CA||y₁-y₂|，结合二次函数的性质可求最小值

解答：解：（1）依题意，设所求的抛物线的方程为：y²=2px（p＞0）
∵焦点A（100，0）
∴

1

2

p=100即p=200
∴所求的抛物线的方程为：y²=400x（p＞0）
（2）设点M（x₁，y₁），N（x₂，y₂）直线MN的方程为x=ny+100
联立

x=ny+100 y2=400x

可得y²-400ny-40000=0
∴y₁+y₂=400n，y₁y₂=-40000
∴|y₁-y₂|=

(y1+y2)2-4y1y2

=400

1+n2

∴S_△CMN=

1

2

|CA||y₁-y₂|=

1

2

×100×400

1+n2

=20000

1+n2

当n=0时，即MN⊥AC时，△CMN的面积最小，最小面积为20000平方米
答：直线通道MN⊥AC时，游乐区CMN的面积最小，最小面积为20000平方米

点评：本题主要考查了由抛物线的性质求解抛物线方程，直线与抛物线位置关系的应用及方程的根与系数关系的应用