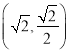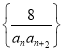题目内容
【题目】（本小题满分12分）已知函数
．
（1）求函数
的最小正周期和单调递增区间；
（2）若在
中，角
，
，
的对边分别为
，
，
，
，
为锐角，且
，求
面积
的最大值．
【答案】（1）最小正周期
，单调递增区间为
；（2）
．
【解析】
试题分析：（1）首先根据二倍角公式以及辅助角公式对
的表达式进行化简：
，从而可知最小正周期
，再根据正弦函数
在
，
上单调递增，从而可令
，解得
，
，即有单调递增区间为；（2）由（1）及条件
可知
，
，从而根据余弦定理
可以得到
，
满足的一个等式：
，再由基本不等式可知
，即有
，从而
，即有
面积的最大值为
．
试题解析：（1），∴最小正周期，令，∴，，即单调递增区间为；（2）由（1）可得：
，
∴
，，，∴由余弦定理可得：，
即
，∴，
∴，当且仅当
时，等号成立，
即
面积的最大值为．
练习册系列答案
孟建平名校考卷系列答案
相关题目
【题目】某花店每天以每枝
元的价格从农场购进若干枝玫瑰花，然后以每枝
元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理．
（I）若花店一天购进
枝玫瑰花，写出当天的利润
（单位：元）关于当天需求量
（单位：枝， 
）的函数解析式．
（II）花店记录了
天玫瑰花的日需求量（单位：枝），整理得下表：
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以
天记录的各需求量的频率作为各需求量发生的概率．
（i）若花店一天购进
枝玫瑰花， 
表示当天的利润（单位：元），求
的分布列，数学期望．
（ii）若花店计划一天购进
枝或
枝玫瑰花，你认为应购进
枝还是
枝？只写结论．
