题目内容
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A= , AB=AC=2A1C1=2,D为BC的中点。
, AB=AC=2A1C1=2,D为BC的中点。
 , AB=AC=2A1C1=2,D为BC的中点。
, AB=AC=2A1C1=2,D为BC的中点。
(1)证明:平面A1AD⊥平面BCC1B1;
(2)求二面角A-CC1-B的大小。
(2)求二面角A-CC1-B的大小。
解:(1)∵ 平面ABC, 平面ABC, 平面ABC, 平面ABC,∴  在  中, 中, ,D为 ,D为 中点 中点∴  又  , ,∴  平面 平面 , ,∵  平面 平面 , ,∴平面  ⊥平面 ⊥平面 。 。 |
|
(2)如图,作 交 交 于 于 点,连接 点,连接 , ,由已知得  平面 平面 ∴  是 是 在面 在面 内的射影 内的射影由三垂线定理知  , ,∴  为二面角 为二面角 的平面角 的平面角过C1作  交 交 于F点, 于F点,则  , , , ,∴  在  中, 中, 在  中,tan∠AEB= 中,tan∠AEB= ∴  , ,即二面角  为 为 。 。 |
 |

练习册系列答案
相关题目
 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,

 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC, ,
, ,AC=2,A1C1=1,
,AC=2,A1C1=1, .
.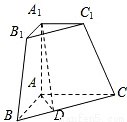 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC, ,
, ,AC=2,A1C1=1,
,AC=2,A1C1=1, .
.