题目内容

设函数f（x）定义域为（a，b），其导函数f'（x）在（a，b）内的图象如图所示，则
f（x）在（a，b）内有极小值的点有______个．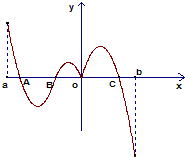
精英家教网
由图象可知导函数f'（x）在（a，b）内有A，B，O，C四个零点，且O点为（0，0）点．
又因为当点x0为极小值点时，f′（x0）=0．
且则当x＞x0的小区间内时，函数f（x）增，f'（x）＞0． 
   当x＜x0的小区间内时，函数f（x）减，f'（x）＜0．
由图可得只有B点满足，故B为极小值点．
故答案为1．
练习册系列答案
相关题目
设函数f（x）定义域为D，若满足①f（x）在D内是单调函数；②存在[a，b]⊆D使f（x）在[a，b]上的值域为[a，b]，那么就称y=f（x）为“成功函数”．若函数g（x）=loga（a2x+t）（a＞0，a≠1）是定义域为R的“成功函数”，则t的取值范围为（　　）
A、（0，+∞）
B、（-∞，0）
C、[0，
1
4
]
D、(0，
1
4
)
设函数f（x）定义域为R，对一切x、y∈R，均满足：f（x+y）+f（x-y）=2f（x）cosy，且f（0）=3，f(
π2
)=4，
（1）求f（π）的值；
（2）求证：f（x）为周期函数，并求出其一个周期；
（3）求函数f（x）解析式．
设函数f（x）定义域为R且f（x）的值恒大于0，对于任意实数x，y，总有f（x+y）=f（x）•f（y），且当x＜0时，f（x）＞1．
（1）求证：f（0）=1，且f（x）在R上单调递减；
（2）设集合A={（x，y）|f（x2）•f（y2）＞f（1）}，B={（x，y）|f（ax-y+2）=1，a∈R}，若A∩B≠∅，求a的取值范围．
设函数f（x）定义域为R，当x＞0时，f（x）＞1，且对任意x，y∈R，有f（x+y）=f（x）•f（y）．
（1）证明：f（0）=1；          
（2）证明：f（x）在R上是增函数；
（3）设集合A={（x，y）|f（x2）•f（y2）＜f（1）}，B={（x，y）|f（x+y+c）=1，c∈R}，若A∩B=φ，求c的取值范围．
设函数f（x）定义域为D，x1，
x
 
2
∈D，同时满足下列条件
①f(x1
x
 
2
)=f(x1)+f(x2)
②
f(x2)-f(x1)
x2-x 1
＞0
③f(
x1+
x
 
2
2
)＞
1
2
[f(x1)+f(x2)]的函数是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网