题目内容
设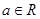 函数
函数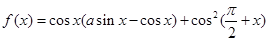 满足
满足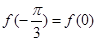 .
.
(1)求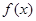 的单调递减区间;
的单调递减区间;
(2)设锐角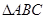 的内角
的内角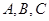 所对的边分别为
所对的边分别为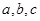 ,且
,且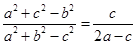 ,求
,求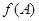 的取值范围.
的取值范围.
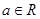 函数
函数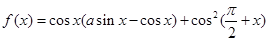 满足
满足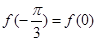 .
.(1)求
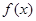 的单调递减区间;
的单调递减区间;(2)设锐角
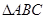 的内角
的内角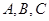 所对的边分别为
所对的边分别为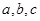 ,且
,且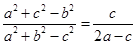 ,求
,求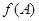 的取值范围.
的取值范围.(1) ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)由
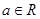 函数
函数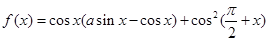 ,运用二倍角公式的逆运算,即可将
,运用二倍角公式的逆运算,即可将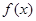 化成一个角的和差的正余弦形式.再结合基本函数的单调性,通过解不等式即可得到
化成一个角的和差的正余弦形式.再结合基本函数的单调性,通过解不等式即可得到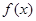 的单调递减区间.
的单调递减区间.(2)因为
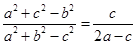 ,结合余弦定理化简后再根据正弦定理,即可得到角B的值,又由(1)所得的函数关系,即可求出角A的范围.
,结合余弦定理化简后再根据正弦定理,即可得到角B的值,又由(1)所得的函数关系,即可求出角A的范围.试题解析:(1)

由
 得:
得: ,∴
,∴ ∴
∴
由
 得:
得: ,
,
∴
 的单调递减区间为:
的单调递减区间为:
(2)∵
 ,由余弦定理得:
,由余弦定理得: ,
,即
 ,由正弦定理得:
,由正弦定理得: ,
, ,
,  ,∴
,∴
∵△
 锐角三角形,∴
锐角三角形,∴ ,
,
∴
 的取值范围为
的取值范围为 .
.
练习册系列答案
相关题目
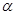 为第三象限角,
为第三象限角,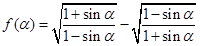 .
.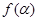 ;
;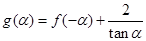 ,求函数
,求函数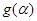 的最小值,并求取最小值时的
的最小值,并求取最小值时的 的定义域为[
的定义域为[ ].
]. 的最小值.
的最小值. 中,
中, ,
, ,边
,边 的长为函数
的长为函数 的最大值,求角
的最大值,求角 大小及
大小及 ,过两点
,过两点 的直线的斜率记为
的直线的斜率记为 .
. 的值;
的值; 的解析式,求
的解析式,求 上的取值范围.
上的取值范围.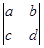 =ad-bc.若cosα=
=ad-bc.若cosα=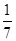 ,
,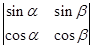 =
=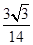 ,0<β<α<
,0<β<α<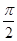 ,则β等于( )
,则β等于( )



 +cos
+cos ·sin
·sin  +
+ sin xcos x(x∈R).
sin xcos x(x∈R). 的值;
的值; =1,求sin B+sin C的最大值.
=1,求sin B+sin C的最大值. ,
, ,则
,则 的值为 .
的值为 . ,
, ,则
,则 的值为 .
的值为 .