题目内容
设双曲线C1:(1)求C1的方程;
(2)求离心率为![]() 的椭圆C2的方程;
的椭圆C2的方程;
(3)设C2的短轴端点为B,求BF中点的轨迹方程.
思路分析:(1)易知a=1,可由P、Q关于x轴对称及正三角形、焦准距这些条件解得b.
(2)设椭圆方程为![]() =1(a1>b1>0).
=1(a1>b1>0).
(3)设B(h,b1),FB中点M(x,y),用参数法,得点M轨迹方程.
解:(1)∵C1过点(1,0)且双曲线方程为![]() =1(a>0,b>0),
=1(a>0,b>0),
∴a=1![]() 双曲线方程为x2-
双曲线方程为x2-![]() =1,右准线l:x=
=1,右准线l:x=![]() 交两条渐近线于点P、Q.可知P、Q关于x轴对称.
交两条渐近线于点P、Q.可知P、Q关于x轴对称.
如下图所示,且P(![]() ,
,![]() ),Q(
),Q(![]() ,-
,-![]() ),而△PQF为正三角形,
),而△PQF为正三角形,

∴|PQ|·![]() =|NF|,
=|NF|,
即![]() ·
·![]() =c-
=c-![]()
![]()
![]() b=c2-1,
b=c2-1,
即c2=![]() b+1. ①
b+1. ①
又c2=1+b2, ②
由①②得b=![]() ,c=2.
,c=2.
故C1:![]() -
-![]() =1.
=1.
(2)由(1)知椭圆离心率e2=![]() =
=![]() =
=![]() .
.
双曲线的左焦点F(2,0),左准线l:x=![]() .
.
根据椭圆的第二定义得
C2: =
=![]() .
.
两边平方,化简得(x-![]() )2+
)2+![]() =1.
=1.
(3)设BF中点M(x,y),由F(2,0),
∴B(2x-2,2y).

由椭圆的第二定义![]() =e2,即
=e2,即 =e2,
=e2,
而e2=![]() =
=![]() .
.
两式消去e2,化简得
4y2-3x+6=0,这就是所求BF中点M的轨迹方程.

练习册系列答案
相关题目
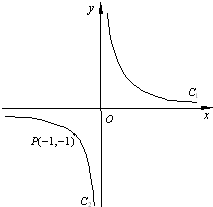 设双曲线xy=1的两支为C1,C2(如图),正三角形PQR的三顶点位于此双曲线上.
设双曲线xy=1的两支为C1,C2(如图),正三角形PQR的三顶点位于此双曲线上.