题目内容

在数列{an}中，

a1=tanx,an+1=.

(1)写出a2,a3,a4;

(2)猜想{an}的通项公式，并加以证明.

解：(1)a2=a3=tan(2·+x),a4=tan(3·+x).

(2)猜想：an=tan［(n-1)·+x］,下1面用数学归纳法证明之：

①当n=1时，显然成立；

②假设n=k时猜想正确，即ak=tan［(k-1)·+x］.

当n=k+1时，ak+1=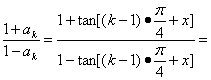tan[+(k-1)·+x]=

tan[(k+1-1)·+x],

故猜想正确.

由①②知对任何n∈N*猜想都正确.


练习册系列答案
相关题目
在数列{an}中，
a
 
1
=1，an=
1
2
an-1+1（n≥2），则数列{an}的通项公式为an=
2-21-n
2-21-n
．
在数列{an}中，a 1=
1
3
，并且对任意n∈N*，n≥2都有an•an-1=an-1-an成立，令bn=
1
an
（n∈N*）．
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）设数列{
an
n
}的前n项和为Tn，证明：
1
3
≤Tn＜
3
4
．
在数列{an}中，a=
12
，前n项和Sn=n2an，求an+1．
在数列{an}中,a1=a,前n项和Sn构成公比为q的等比数列,________________.

(先在横线上填上一个结论,然后再解答)

在数列{an}中，a，并且对任意n∈N*，n≥2都有an•an-1=an-1-an成立，令bn=（n∈N*）．
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）设数列{}的前n项和为Tn，证明：．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网