题目内容
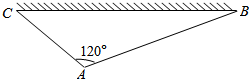
15.如图,某小区进行绿化改造,计划围出一块三角形绿地ABC,其中一边利用现成的围墙BC,长度为a米,另外两边AB,AC使用某种新型材料,∠BAC=120°,设AB=x米,AC=y米.(1)求x,y满足的关系式;
(2)若无论如何设计上述三角形绿地确保此材料都够用,则至少需准备长度为多少的此种新型材料?
分析 (1)利用余弦定理得出x,y的关系;
(2)利用正弦定理将x,y表示为B的函数,求出x+y的最大值即可.
解答 解:(1)由余弦定理得BC2=AC2+AB2-2AB•ACcosA,
即a2=x2+y2+xy,
∴x,y满足的关系式为x2+y2+xy=a2.
(2)∵A=120°,∴C=60°-B.
由正弦定理得$\frac{a}{sinA}=\frac{x}{sinC}=\frac{y}{sinB}$,
∴x=$\frac{2\sqrt{3}a}{3}sin$(60°-B)=acosB-$\frac{\sqrt{3}}{3}$asinB,y=$\frac{2\sqrt{3}a}{3}sinB$.
∴x+y=acosB+$\frac{\sqrt{3}}{3}a$sinB=$\frac{2\sqrt{3}}{3}$a($\frac{\sqrt{3}}{2}$cosB+$\frac{1}{2}$sinB)=$\frac{2\sqrt{3}}{3}$asin(B+60°).
∵0°<B<60°,∴60°<B+60°<120°,
∴当B+60°=90°时,x+y取得最大值$\frac{2\sqrt{3}}{3}a$.
∴至少需准备长度为$\frac{2\sqrt{3}}{3}a$的此种新型材料才能确保无论如何设计都能够用.
点评 本题考查了正弦定理,余弦定理,正弦函数的图象与性质,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
7.过双曲线C:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1右焦点F作一直线(不平行于坐标轴)交双曲线于A、B两点,若点M满足条件$\overrightarrow{MA}$+$\overrightarrow{MB}$=$\overrightarrow{0}$,O为坐标原点,则kAB•kOM的值为( )
| A. | $\frac{5}{4}$ | B. | -$\frac{5}{4}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
9.若点P(3,y)是角α终边上的一点,且满足y<0,cosα=$\frac{3}{5}$,则tanα=( )
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
10.过点(1,-1)且与曲线y=x3-2x相切的切线方程为( )
| A. | x-y-2=0或5x+4y-1=0 | B. | x-y-2=0 | ||
| C. | x-y+2=0 | D. | x-y-2=0或4x+5y+1=0 |
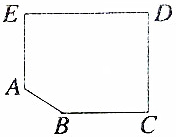 某小区内有一块荒地ABCDE,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发(如图所示),问如何设计才能使开发的面积最大?最大开发面积是多少?(已知BC=210m,CD=240m,DE=300m,EA=180m)
某小区内有一块荒地ABCDE,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发(如图所示),问如何设计才能使开发的面积最大?最大开发面积是多少?(已知BC=210m,CD=240m,DE=300m,EA=180m)