题目内容
已知过椭圆C: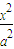 +
+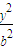 =1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数y=asinx+3bcosx图象的一条对称轴的方程是
=1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数y=asinx+3bcosx图象的一条对称轴的方程是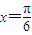 .(1)求椭圆C的离心率e与直线AB的方程;(2)对于任意一点M∈C,试证:总存在角θ(θ∈R)使等式
.(1)求椭圆C的离心率e与直线AB的方程;(2)对于任意一点M∈C,试证:总存在角θ(θ∈R)使等式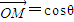
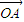 +sinθ
+sinθ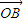 成立.
成立.
【答案】分析:(1)通过函数图象的一条对称轴的方程是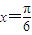 .推出f(
.推出f(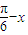 )=f(
)=f(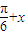 ),利用取
),利用取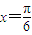 ,整理得a=
,整理得a= b,求出离心率,求出焦点坐标然后求出直线方程;
b,求出离心率,求出焦点坐标然后求出直线方程;
(2))利用 与
与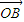 是平面内的两个不共线的向量,由平面向量的基本定理,表示
是平面内的两个不共线的向量,由平面向量的基本定理,表示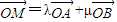 ,设M(x,y),通过坐标运算,推出x=λx1+μx2,y=λy1+μy2.代入椭圆方程,推出x1x2+3y1y2=0,由A,B两点在椭圆上,整理出λ2+μ2=1.根据圆的参数方程可知,总存在角θ,θ∈R使等式
,设M(x,y),通过坐标运算,推出x=λx1+μx2,y=λy1+μy2.代入椭圆方程,推出x1x2+3y1y2=0,由A,B两点在椭圆上,整理出λ2+μ2=1.根据圆的参数方程可知,总存在角θ,θ∈R使等式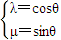 成立,就是
成立,就是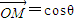
 +sinθ
+sinθ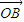 成立.
成立.
得到结论.
解答:解:(1)函数y=asinx+3bcosx图象的一条对称轴的方程是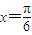 .所以对任意的实数x都有f(
.所以对任意的实数x都有f( )=f(
)=f(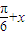 ),
),
取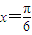 得f(0)=f(
得f(0)=f( ),整理得a=
),整理得a=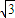 b,
b,
则椭圆的方程为x2+3y2=3b2…①.
于是椭圆C的离心率e=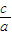 =
=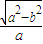 =
=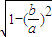 =
=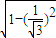 =
=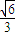 .
.
又椭圆的右焦点F(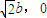 )
)
因为过椭圆C: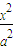 +
+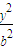 =1(a>b>0)右焦点F且斜率为1的直线,
=1(a>b>0)右焦点F且斜率为1的直线,
∴直线AB的方程为:y=x-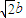 .
.
(2)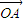 与
与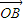 是平面内的两个不共线的向量,由平面向量的基本定理,对于这一平面内的向量
是平面内的两个不共线的向量,由平面向量的基本定理,对于这一平面内的向量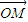 ,有且只有一对实数λ,μ.使得
,有且只有一对实数λ,μ.使得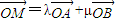 成立.
成立.
设M(x,y),则(x,y)=λ(x1,y1)+μ(x2+y2).
∴x=λx1+μx2,y=λy1+μy2.
又M∈C,代入①式得(λx1+μx2)2+3(λy1+μy2)2=3b2,
展开整理得λ2(x12+3y12)+μ2(x22+3y22)+2λμ(x1x2+3y1y2)=3b2…②
由AB的方程可知x1x2+3y1y2=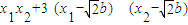
=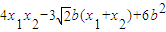 =3b2-9b2+6b2=0.
=3b2-9b2+6b2=0.
由A,B两点在椭圆上,所以x12+3y12=3b2.x22+3y22=3b2.
代入②式化简得λ2+μ2=1.
根据圆的参数方程可知,总存在角θ,θ∈R使等式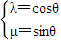 成立.
成立.
即: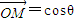
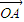 +sinθ
+sinθ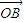 成立.
成立.
综上所述,对于任意一点M∈C,总存在角θ(θ∈R)使等式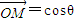
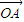 +sinθ
+sinθ 成立.
成立.
点评:本题要求学生熟练运用构造角化简三角函数asinx+3bcosx,并熟练应用直线与圆锥曲线相交弦问题的解题方程,能够灵活运用设点法、韦达定理整体思想.简化运算:熟练运用平面向量基本定理和向量的坐标运算.考查计算能力,转化思想.
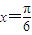 .推出f(
.推出f(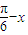 )=f(
)=f(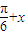 ),利用取
),利用取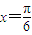 ,整理得a=
,整理得a= b,求出离心率,求出焦点坐标然后求出直线方程;
b,求出离心率,求出焦点坐标然后求出直线方程;(2))利用
 与
与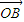 是平面内的两个不共线的向量,由平面向量的基本定理,表示
是平面内的两个不共线的向量,由平面向量的基本定理,表示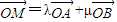 ,设M(x,y),通过坐标运算,推出x=λx1+μx2,y=λy1+μy2.代入椭圆方程,推出x1x2+3y1y2=0,由A,B两点在椭圆上,整理出λ2+μ2=1.根据圆的参数方程可知,总存在角θ,θ∈R使等式
,设M(x,y),通过坐标运算,推出x=λx1+μx2,y=λy1+μy2.代入椭圆方程,推出x1x2+3y1y2=0,由A,B两点在椭圆上,整理出λ2+μ2=1.根据圆的参数方程可知,总存在角θ,θ∈R使等式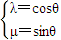 成立,就是
成立,就是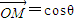
 +sinθ
+sinθ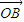 成立.
成立.得到结论.
解答:解:(1)函数y=asinx+3bcosx图象的一条对称轴的方程是
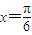 .所以对任意的实数x都有f(
.所以对任意的实数x都有f( )=f(
)=f(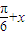 ),
),取
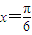 得f(0)=f(
得f(0)=f( ),整理得a=
),整理得a=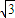 b,
b,则椭圆的方程为x2+3y2=3b2…①.
于是椭圆C的离心率e=
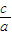 =
=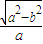 =
=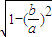 =
=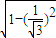 =
=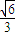 .
.又椭圆的右焦点F(
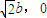 )
)因为过椭圆C:
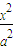 +
+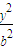 =1(a>b>0)右焦点F且斜率为1的直线,
=1(a>b>0)右焦点F且斜率为1的直线,∴直线AB的方程为:y=x-
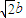 .
.(2)
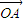 与
与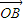 是平面内的两个不共线的向量,由平面向量的基本定理,对于这一平面内的向量
是平面内的两个不共线的向量,由平面向量的基本定理,对于这一平面内的向量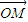 ,有且只有一对实数λ,μ.使得
,有且只有一对实数λ,μ.使得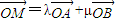 成立.
成立.设M(x,y),则(x,y)=λ(x1,y1)+μ(x2+y2).
∴x=λx1+μx2,y=λy1+μy2.
又M∈C,代入①式得(λx1+μx2)2+3(λy1+μy2)2=3b2,
展开整理得λ2(x12+3y12)+μ2(x22+3y22)+2λμ(x1x2+3y1y2)=3b2…②
由AB的方程可知x1x2+3y1y2=
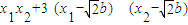
=
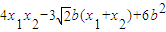 =3b2-9b2+6b2=0.
=3b2-9b2+6b2=0.由A,B两点在椭圆上,所以x12+3y12=3b2.x22+3y22=3b2.
代入②式化简得λ2+μ2=1.
根据圆的参数方程可知,总存在角θ,θ∈R使等式
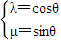 成立.
成立.即:
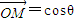
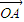 +sinθ
+sinθ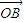 成立.
成立.综上所述,对于任意一点M∈C,总存在角θ(θ∈R)使等式
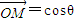
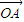 +sinθ
+sinθ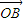 成立.
成立.点评:本题要求学生熟练运用构造角化简三角函数asinx+3bcosx,并熟练应用直线与圆锥曲线相交弦问题的解题方程,能够灵活运用设点法、韦达定理整体思想.简化运算:熟练运用平面向量基本定理和向量的坐标运算.考查计算能力,转化思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
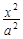 +
+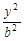 =1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数
=1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数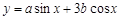 图象的一条对称轴的方程是
图象的一条对称轴的方程是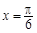 .
.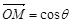
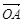 +
+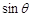
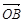 成立.
成立.