题目内容
10.若$\overrightarrow{a}$,$\overrightarrow{b}$均为单位向量,且$\overrightarrow{a}$•$\overrightarrow{b}$=0,($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=0,则|$\overrightarrow{c}$|的最大值为$\sqrt{2}$.分析 已知$\overrightarrow{a}$,$\overrightarrow{b}$均为单位向量,且$\overrightarrow{a}$•$\overrightarrow{b}$=0,不妨设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=(x,y),利用($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=0,化简得到关于x,y的等式,可求|$\overrightarrow{c}$|的最大值.
解答 解:已知$\overrightarrow{a}$,$\overrightarrow{b}$均为单位向量,且$\overrightarrow{a}$•$\overrightarrow{b}$=0,不妨设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=(x,y),由($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=0,得到x2-x+y2-y=0
它表示以($\frac{1}{2}$,$\frac{1}{2}$)为圆心,$\frac{\sqrt{2}}{2}$为半径的圆,可知|$\overrightarrow{c}$|的最大值是$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查平面向量数量积的运算,向量的模的几何意义,高考常考点,是中档题.

| A. | 7 | B. | $\frac{1}{7}$ | C. | -7 | D. | $-\frac{1}{7}$ |
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |

| A. | i≤2012 | B. | i>2012 | C. | i≤1006 | D. | i>1006 |
| A. | p2 | B. | (1-p)2 | C. | np | D. | p2(1-p) |
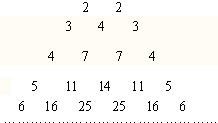 如图,它满足(1)第n行首尾两数均为n,
如图,它满足(1)第n行首尾两数均为n,