题目内容
已知数列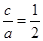 ,其前
,其前 项和为
项和为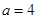 .
.
⑴若对任意的 ,
,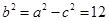 组成公差为
组成公差为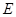 的等差数列,且
的等差数列,且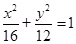 ,
,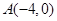 ,求
,求 的值;
的值;
⑵若数列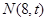 是公比为
是公比为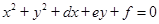 的等比数列,
的等比数列,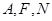 为常数,求证:数列
为常数,求证:数列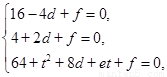 为等比数列的充要条件为
为等比数列的充要条件为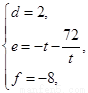 .
.
【答案】
(1)
(2)证明充要条件命题,要证明充分性和必要性同时成立即可。
【解析】
试题分析:⑴因为 成公差为
成公差为 的等差数列,
的等差数列,
所以 ,
2分
,
2分
所以 是公差为
是公差为 的等差数列,且
的等差数列,且
 ,
4分
,
4分
又因为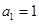 ,所以
,所以
 ,
,
所以 ,所以
,所以 .
6分
.
6分
⑵因为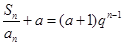 ,所以
,所以 , ①
, ①
所以 , ②
, ②
②-①,得 ,
③ 8分
,
③ 8分
(ⅰ)充分性:因为 ,所以
,所以 ,代入③式,得
,代入③式,得
 ,因为
,因为 ,又
,又 ,
,
所以 ,
, ,所以
,所以 为等比数列,
12分
为等比数列,
12分
(ⅱ)必要性:设 的公比为
的公比为 ,则由③得
,则由③得 ,
,
整理得 ,
14分
,
14分
此式为关于n的恒等式,若 ,则左边
,则左边 ,右边
,右边 ,矛盾;
,矛盾;
 ,当且仅当
,当且仅当 时成立,所以
时成立,所以 .
.
由(ⅰ)、(ⅱ)可知,数列 为等比数列的充要条件为
为等比数列的充要条件为 .
16分
.
16分
考点:等比数列的概念,等差数列
点评:主要是考查了等差数列求和以及通项公式的运用,和等比数列的概念的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
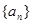 ,其前
,其前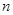 项和为
项和为 .
.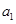 ,
,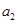 ;
; 满足
满足 ,请证明数列
,请证明数列 .
. ,其前
,其前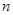 项和为
项和为 ,对任意
,对任意 都有:
都有:
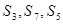 构成等差数列,求实数
构成等差数列,求实数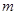 的值;
的值;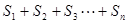 ,
,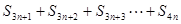 ,
, 不能构成等差数列.
不能构成等差数列.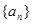 ,其前
,其前 项和为
项和为 .
.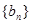 满足
满足 ,请证明数列
,请证明数列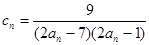 ,数列
,数列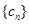 的前
的前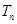 ,求使不等式
,求使不等式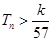 对一切
对一切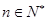 都成立的最大正整数
都成立的最大正整数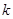 的值.
的值.