题目内容
(本题满分16分)
已知数列 ,其前
,其前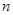 项和为
项和为 ,对任意
,对任意 都有:
都有:
(1)求证: 是等比数列;
是等比数列;
(2)若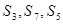 构成等差数列,求实数
构成等差数列,求实数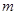 的值;
的值;
(3)求证:对任意大于1的实数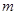 ,
,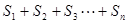 ,
,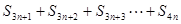 ,
,
 不能构成等差数列.
不能构成等差数列.
【答案】
(1)当 时,
时, ,又
,又 ,故
,故
当 时,
时, ,故
,故 ,即
,即 ,
,
也即
所以, 是以
是以 为首项,
为首项, 为公比的等比数列;
为公比的等比数列;
(2)由 构成等差数列,知:
构成等差数列,知:
即 =
=  +
+ ,又
,又 ,化简得:
,化简得:
令
 ,则
,则 ,得
,得 或
或 (舍),即
(舍),即 (舍),
(舍),
由
 ,解得,
,解得, ,
,
(1) (3)假设 ,
, ,
,
 构成等差数列,
构成等差数列,
则2( )=(
)=( )+(
)+( )
)
即 =
=
 +
+
化简得 =
= +
+ ,又知
,又知 ,
, ,
,
可得 =
= +
+ (*)
(*)
而 ,所以
,所以 ,
, ,且
,且 ,故(*)无解
,故(*)无解
所以假设错误,也即对任意大于1的实数 ,
, ,
, ,
,
 不能构成等差数列.
不能构成等差数列.
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在