题目内容
抛物线y2=4x上一点A到点B(3,2)与焦点的距离之和最小,则点A的坐标为 .
分析:由抛物线y2=4x可得焦点F(1,0),直线l的方程:x=-1.如图所示,过点A作AM⊥l,垂足为M.由定义可得|AM|=|AF|.因此当三点B,A,M共线时,|AB|+|AM|=|BM|取得最小值.yA,代入抛物线方程可得xA.
解答:解:由抛物线y2=4x可得焦点F(1,0),直线l的方程:x=-1.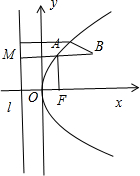
如图所示,过点A作AM⊥l,垂足为M.则|AM|=|AF|.
因此当三点B,A,M共线时,|AB|+|AM|=|BM|取得最小值3-(-1)=4.
此时yA=2,代入抛物线方程可得22=4xA,解得xA=1.
∴点A(1,2).
故答案为:(1,2).

如图所示,过点A作AM⊥l,垂足为M.则|AM|=|AF|.
因此当三点B,A,M共线时,|AB|+|AM|=|BM|取得最小值3-(-1)=4.
此时yA=2,代入抛物线方程可得22=4xA,解得xA=1.
∴点A(1,2).
故答案为:(1,2).
点评:本题考查了抛物线的定义、标准方程及其性质、最小值问题,属于中档题.

练习册系列答案
相关题目