题目内容
已知函数f(x)=2
sinxcosx+cos2x+1(x∈R).
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)求函数f(x)在[-
,
]上的最小值,并写出f(x)取最小值时相应的x值.
| 3 |
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)求函数f(x)在[-
| π |
| 4 |
| π |
| 4 |
考点:三角函数中的恒等变换应用,正弦函数的单调性
专题:计算题,三角函数的求值
分析:(Ⅰ)利用二倍角、辅助角公式化简函数,结合正弦函数的单调性,即可求函数f(x)的单调递增区间;
(Ⅱ)因为x∈[-
,
],所以2x+
∈[-
,
],利用三角函数的性质,即可求得结论.
(Ⅱ)因为x∈[-
| π |
| 4 |
| π |
| 4 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
解答:
解:(Ⅰ)f(x)=2
sinxcosx+cos2x+1=
sin2x+cos2x+1=2sin(2x+
)+1,
由2x+
∈[-
+2kπ,
+2kπ],可得x∈[-
+kπ,
+kπ](k∈Z).
∴函数的单调递增区间为[-
+kπ,
+kπ](k∈Z). …(7分)
(Ⅱ)∵x∈[-
,
],
∴2x+
∈[-
,
]…(9分),
∴-
+1≤2sin(2x+
)+1≤3,…(11分)
∴当2x+
=-
,即x=-
时,函数f(x)取得最小值-
+1.…(13分)
| 3 |
| 3 |
| π |
| 6 |
由2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
∴函数的单调递增区间为[-
| π |
| 3 |
| π |
| 6 |
(Ⅱ)∵x∈[-
| π |
| 4 |
| π |
| 4 |
∴2x+
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
∴-
| 3 |
| π |
| 6 |
∴当2x+
| π |
| 6 |
| π |
| 3 |
| π |
| 4 |
| 3 |
点评:本题考查三角函数的化简,考查三角函数的性质,考查学生的计算能力,正确化简函数是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=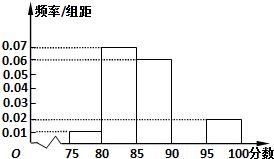 某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.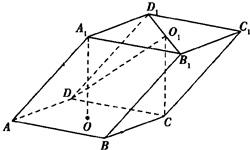 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1、O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1、O分别为上、下底面的中心,且A1在底面ABCD上的射影是O. 如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2
如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2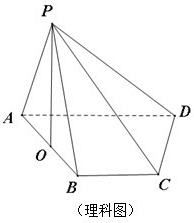 (理科做)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠ABC=90°,BC∥AD,且AB=AD=2BC,顶点P在底面ABCD内的射影恰好落在AB的中点O上.
(理科做)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠ABC=90°,BC∥AD,且AB=AD=2BC,顶点P在底面ABCD内的射影恰好落在AB的中点O上.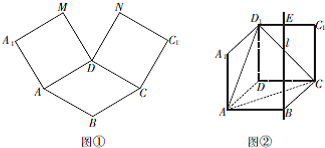 如图①,在平面内,ABCD是∠BAD=60°且AB=a的菱形,ADMA1和CDNC1都是正方形. 将两个正方形分别沿AD,CD折起,使M与N重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图②).
如图①,在平面内,ABCD是∠BAD=60°且AB=a的菱形,ADMA1和CDNC1都是正方形. 将两个正方形分别沿AD,CD折起,使M与N重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图②).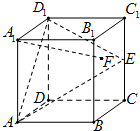 在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值的取值范围是
在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值的取值范围是