题目内容
已知A1,A2分别是双曲线E:
-
=1的左、右顶点,P为直线x=
c(c为半焦距)上的一点,△A2PA1是底角为30°的等腰三角形,则双曲线E的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
分析:作出图形,根据题设条件,利用数形结合思想,能够求出双曲线E的离心率.
解答: 解:∵A1,A2分别是双曲线E:
解:∵A1,A2分别是双曲线E:
-
=1的左、右顶点,P为直线x=
c(c为半焦距)上的一点,
△A2PA1是底角为30°的等腰三角形,
∴|A1A2|=|PA2|=2a,
设直线x=
c交x轴于点B,则∠PA2B=60°,
∴|A2B|=
|A2P|=a,
∴2a=
c,即3c=4a,
∴e=
=
.
故选B.
 解:∵A1,A2分别是双曲线E:
解:∵A1,A2分别是双曲线E:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
△A2PA1是底角为30°的等腰三角形,
∴|A1A2|=|PA2|=2a,
设直线x=
| 3 |
| 2 |
∴|A2B|=
| 1 |
| 2 |
∴2a=
| 3 |
| 2 |
∴e=
| c |
| a |
| 4 |
| 3 |
故选B.
点评:本题考查双曲线的离心率的求法,解题时要认真审题,熟练掌握基本概念和基础知识,注意数形结合思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
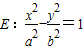 的左、右顶点,P为直线
的左、右顶点,P为直线 (c为半焦距)上的一点,△A2PA1是底角为30°的等腰三角形,则双曲线E的离心率为( )
(c为半焦距)上的一点,△A2PA1是底角为30°的等腰三角形,则双曲线E的离心率为( )


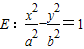 的左、右顶点,P为直线
的左、右顶点,P为直线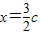 (c为半焦距)上的一点,△A2PA1是底角为30°的等腰三角形,则双曲线E的离心率为( )
(c为半焦距)上的一点,△A2PA1是底角为30°的等腰三角形,则双曲线E的离心率为( )


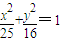 的左、右顶点,P是过左焦点F且垂直于A1A2的直线l上的一点,则
的左、右顶点,P是过左焦点F且垂直于A1A2的直线l上的一点,则 = .
= .