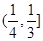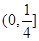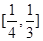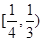题目内容
函数 是( )
是( )
A.奇函数且在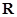 上是减函数 上是减函数 | B.奇函数且在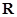 上是增函数 上是增函数 |
C.偶函数且在 上是减函数 上是减函数 | D.偶函数且在 上是增函数 上是增函数 |
B
解析试题分析:因为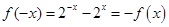 ,所以函数
,所以函数 是奇函数.又函数
是奇函数.又函数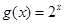 与函数
与函数 都是
都是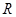 上的增函数,所以由简单复合函数的单调性可知,
上的增函数,所以由简单复合函数的单调性可知,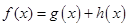 也是
也是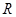 上的增函数.
上的增函数.
考点:1.偶函数;2.简单复合函数的单调性

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
函数 的定义域是 ( )
的定义域是 ( )
A.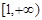 | B.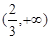 | C.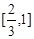 | D.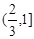 |
函数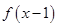 是
是 上的奇函数,
上的奇函数,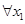 、
、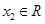 ,
,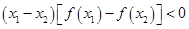 ,则
,则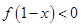 的解集是( )
的解集是( )
A.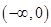 | B.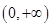 | C. | D.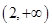 |
设奇函数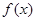 满足
满足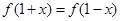 ,当
,当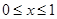 时,
时,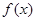 =
=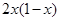 ,则
,则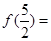 ( )
( )
A.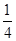 | B.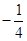 | C.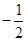 | D.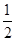 |
已知函数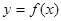 是R上的偶函数,对于
是R上的偶函数,对于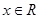 都有
都有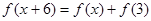 成立,且
成立,且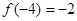 ,当
,当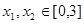 ,且
,且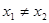 时,都有
时,都有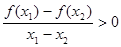 .则给出下列命题:
.则给出下列命题:
①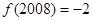 ; ②函数
; ②函数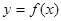 图象的一条对称轴为
图象的一条对称轴为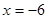 ;
;
③函数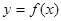 在[﹣9,﹣6]上为减函数; ④方程
在[﹣9,﹣6]上为减函数; ④方程 在[﹣9,9]上有4个根;
在[﹣9,9]上有4个根;
其中正确的命题个数为( )
| A.1 | B.2 | C.3 | D.4 |
偶函数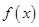 在
在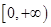 上为减函数,不等式
上为减函数,不等式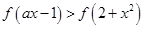 恒成立,则
恒成立,则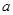 的取值范围是( )
的取值范围是( )
A.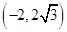 | B.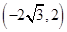 | C.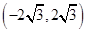 | D.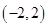 |
定义在R上的可导函数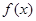 ,已知
,已知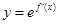 的图象如图所示,则
的图象如图所示,则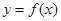 的增区间是( )
的增区间是( )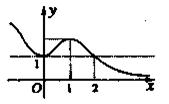
A.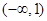 | B.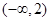 | C.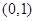 | D.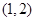 |
函数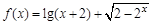 的定义域为( )
的定义域为( )
A.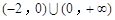 | B.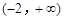 |
C.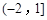 | D.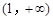 |
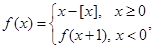 其中
其中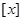 表示不超过
表示不超过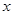 的最大整数,如
的最大整数,如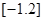 =-2,
=-2,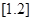 =1,
=1,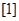 =1,
=1,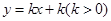 与函数y=
与函数y= 的图象恰有三个不同的交点,则
的图象恰有三个不同的交点,则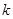 的取值范围是 ( )
的取值范围是 ( )