题目内容
已知函数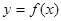 是R上的偶函数,对于
是R上的偶函数,对于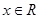 都有
都有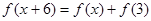 成立,且
成立,且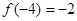 ,当
,当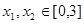 ,且
,且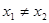 时,都有
时,都有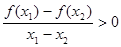 .则给出下列命题:
.则给出下列命题:
①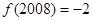 ; ②函数
; ②函数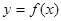 图象的一条对称轴为
图象的一条对称轴为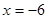 ;
;
③函数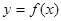 在[﹣9,﹣6]上为减函数; ④方程
在[﹣9,﹣6]上为减函数; ④方程 在[﹣9,9]上有4个根;
在[﹣9,9]上有4个根;
其中正确的命题个数为( )
| A.1 | B.2 | C.3 | D.4 |
D
解析试题分析:令 ,由
,由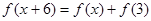 得
得 ,又函数
,又函数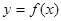 是R上的偶函数,所以
是R上的偶函数,所以 .
. .即函数
.即函数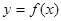 是以6为周期的周期函数.所以
是以6为周期的周期函数.所以 .又
.又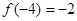 ,所以
,所以 ,从而
,从而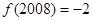 ;又函数关于
;又函数关于 轴对称.周期为6,所以函数
轴对称.周期为6,所以函数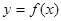 图象的一条对称轴为
图象的一条对称轴为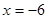 ;又当
;又当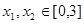 ,且
,且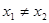 时,都有
时,都有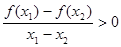 ,设
,设 ,则
,则 .故易知函数
.故易知函数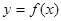 在
在 上是增函数.根据对称性,易知函数
上是增函数.根据对称性,易知函数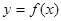 在
在 上是减函数,又根据周期性,函数
上是减函数,又根据周期性,函数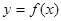 在[﹣9,﹣6]上为减函数;因为
在[﹣9,﹣6]上为减函数;因为 ,又由其单调性及周期性,可知在[﹣9,9],有且仅有
,又由其单调性及周期性,可知在[﹣9,9],有且仅有 ,即方程
,即方程 在[﹣9,9]上有4个根.综上所述,四个命题都正确.
在[﹣9,9]上有4个根.综上所述,四个命题都正确.
考点:函数的奇偶性、函数的单调性与周期性、函数的零点与方程的根

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
函数y=f(x)在区间(-2,2)上的图象是连续的,且方程f(x)=0在(-2,2)上仅有一个实根0,则f(-1)·f(1)的值( )
| A.大于0 | B.小于0 |
| C.等于0 | D.无法确定 |
函数 是( )
是( )
A.奇函数且在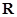 上是减函数 上是减函数 | B.奇函数且在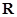 上是增函数 上是增函数 |
C.偶函数且在 上是减函数 上是减函数 | D.偶函数且在 上是增函数 上是增函数 |
已知函数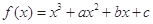 有两个极值点
有两个极值点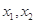 ,若
,若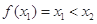 ,则关于
,则关于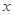 的方程
的方程 的不同实根个数为( )
的不同实根个数为( )
| A.3 | B.4 | C.5 | D.6 |
已知函数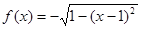 ,若
,若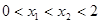 ,则( )
,则( )
A.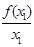 > > 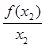 | B.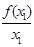 = = 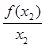 |
C.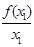 < < 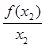 | D.无法判断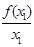 与 与 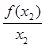 的大小 的大小 |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A. | B.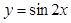 | C.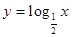 | D. |
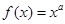 满足
满足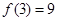 ,那么函数
,那么函数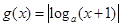 的图象大致为( )
的图象大致为( )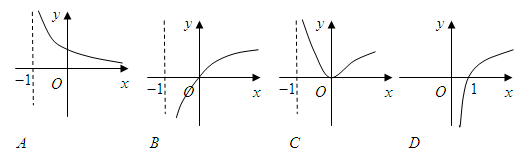
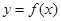 对任意的
对任意的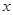 都满足
都满足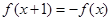 ,当
,当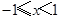 时,
时,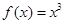 ,若函数
,若函数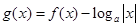 至少6个零点,则
至少6个零点,则 取值范围是( )
取值范围是( )
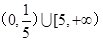
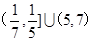
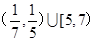
 的图像是:( )
的图像是:( )