题目内容
函数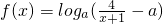 在[0,1]上是减函数,则a的取值范围为________.
在[0,1]上是减函数,则a的取值范围为________.
(1,2)
分析:当0<a<1时,根据复合函数的单调性规律检验不满足条件,当a>1时,根据复合函数的单调性规律检验满足条件.再由对数函数的定义域可得x=1时,对数的真数大于零,综合可得a的取值范围.
解答:根据函数t= 在[0,1]上是减函数,函数
在[0,1]上是减函数,函数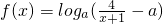 在[0,1]上是增函数,故a>1.
在[0,1]上是增函数,故a>1.
又当x=1时,函数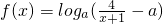 有意义,故有
有意义,故有 >0,解得 a<2.
>0,解得 a<2.
综上可得 1<a<2,
故答案为 (1,2).
点评:本题主要考查对数函数的单调性和特殊点,对数函数的定义域,复合函数的单调性规律,属于中档题.
分析:当0<a<1时,根据复合函数的单调性规律检验不满足条件,当a>1时,根据复合函数的单调性规律检验满足条件.再由对数函数的定义域可得x=1时,对数的真数大于零,综合可得a的取值范围.
解答:根据函数t=
 在[0,1]上是减函数,函数
在[0,1]上是减函数,函数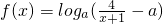 在[0,1]上是增函数,故a>1.
在[0,1]上是增函数,故a>1.又当x=1时,函数
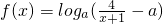 有意义,故有
有意义,故有 >0,解得 a<2.
>0,解得 a<2.综上可得 1<a<2,
故答案为 (1,2).
点评:本题主要考查对数函数的单调性和特殊点,对数函数的定义域,复合函数的单调性规律,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 满足:①函数
满足:①函数 的图象关于直线
的图象关于直线 对称;②
对称;②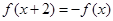 ;③
;③ 上是增函数。下列关于
上是增函数。下列关于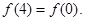
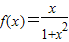 .
.