题目内容
【题目】已知函数![]() ,函数
,函数![]() .
.
![]() Ⅰ
Ⅰ![]() 若函数
若函数![]() 在
在![]() 和
和![]() 上单调性相反,求
上单调性相反,求![]() 的解析式;
的解析式;
![]() Ⅱ
Ⅱ![]() 若
若![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求a的取值范围;
上恒成立,求a的取值范围;
![]() Ⅲ
Ⅲ![]() 已知
已知![]() ,若函数
,若函数![]() 在区间
在区间![]() 内有且只有一个零点,试确定实数a的范围.
内有且只有一个零点,试确定实数a的范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 若函数
若函数![]() 在
在![]() 和
和![]() 上单调性相反,得到
上单调性相反,得到![]() 是对称轴,进行求解即可求
是对称轴,进行求解即可求![]() 的分析式;
的分析式;
![]() Ⅱ
Ⅱ![]() 利用参数分离法将不等式
利用参数分离法将不等式![]() 在
在![]() 上恒成立转化为求最值问题即可,求a的取值范围;
上恒成立转化为求最值问题即可,求a的取值范围;
![]() Ⅲ
Ⅲ![]() 根据函数零点和方程之间的关系,判断函数的单调性,即可得到结论.
根据函数零点和方程之间的关系,判断函数的单调性,即可得到结论.
![]() Ⅰ
Ⅰ![]() 由单调性知,函数
由单调性知,函数![]() 为二次函数,
为二次函数,
其对称轴为![]() ,解得
,解得![]() ,
,
![]() 所求
所求![]()
![]() Ⅱ
Ⅱ![]() 依题意得
依题意得![]() ,
,
即![]() 在
在![]() 上恒成立,
上恒成立,
转化为![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上恒成立,
上恒成立,
转化为![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,则转化为
,则转化为![]() 在
在![]() 上恒成立
上恒成立
即![]() ,
,![]() 所以
所以![]()
![]() Ⅲ
Ⅲ![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
则原命题等价于两个函数![]() 与
与![]() 的图象在区间
的图象在区间![]() 内有唯一交点.
内有唯一交点.
当![]() 时,
时,![]() 在
在![]() 内为减函数,
内为减函数,![]() ,
,![]() 为增函数,
为增函数,
且![]() ,
,![]() ,
,![]() 函数在区间有唯一的交点;
函数在区间有唯一的交点;
当![]() 时,
时,![]() 图象开口向下,对称轴为
图象开口向下,对称轴为![]() ,
,
![]() 在
在![]() 内为减函数,
内为减函数,![]() ,
,![]() 为增函数,
为增函数,
且![]() ,
,
![]() .
.
当![]() 时,
时,![]() 图象开口向上,对称轴为
图象开口向上,对称轴为![]() ,
,
![]() 在
在![]() 内为减函数,
内为减函数,![]() ,
,![]() 为增函数,
为增函数,
则由![]() ,
,
![]() .
.
综上,所求a的取值范围为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】甲、乙两人在相同条件下各打靶10次,每次打靶所得的环数如图所示.
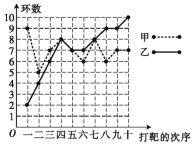
填写下表,请从下列角度对这次结果进行分析.
命中9环及以上的次数 | 平均数 | 中位数 | 方差 | |
甲 | ||||
乙 |
(1)命中9环及以上的次数(分析谁的成绩好些);
(2)平均数和中位数(分析谁的成绩好些);
(3)方差(分析谁的成绩更稳定);
(4)折线图上两人射击命中环数的走势(分析谁更有潜力).


