题目内容
3.已知函数f(x)=$\left\{{\begin{array}{l}{sin\frac{πx}{2},x≤0}\\{\frac{1}{6}-{{log}_3}x,x>0}\end{array}}$,则$f[{f({3\sqrt{3}})}]$=-$\frac{\sqrt{3}}{2}$.分析 先求出f(3$\sqrt{3}$)=-$\frac{4}{3}$,从而$f[{f({3\sqrt{3}})}]$=f(-$\frac{4}{3}$),由此能求出结果.
解答 解:∵函数f(x)=$\left\{{\begin{array}{l}{sin\frac{πx}{2},x≤0}\\{\frac{1}{6}-{{log}_3}x,x>0}\end{array}}$,
∴f(3$\sqrt{3}$)=$\frac{1}{6}-lo{g}_{3}3\sqrt{3}$=$\frac{1}{6}-\frac{3}{2}$=-$\frac{4}{3}$,
$f[{f({3\sqrt{3}})}]$=f(-$\frac{4}{3}$)=sin([$\frac{π}{2}×(-\frac{4}{3})$]=-sin$\frac{2π}{3}$=-sin$\frac{π}{3}$=-$\frac{\sqrt{3}}{2}$.
故答案为:$-\frac{{\sqrt{3}}}{2}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
13.已知全集U={1,2,3,4,5,6},A={1,3,5},B={2,3,4},则(∁UA)∩B=( )
| A. | {2,4} | B. | { 3 } | C. | {2,4,6} | D. | {1,2,3,4,5} |
11.下列命题正确的是( )
| A. | 若x≠kπ,k∈Z,则 sin2x+$\frac{2}{si{n}^{2}x}$≥2$\sqrt{2}$ | B. | 若a<0,则a+$\frac{4}{a}$≥-4 | ||
| C. | 若a>0,b>0,则lga+lgb$≥2\sqrt{lga•lgb}$ | D. | 若a<0,b<0,则$\frac{a}{b}+\frac{b}{a}≥2$ |
18. 函数f(x)=sin(ωx+φ)(其中ω>0且|φ|≤$\frac{π}{2}$)的图象如图所示,为了得到y=sinωx的图象,只需把y=f(x)的图象上所有点( )
函数f(x)=sin(ωx+φ)(其中ω>0且|φ|≤$\frac{π}{2}$)的图象如图所示,为了得到y=sinωx的图象,只需把y=f(x)的图象上所有点( )
 函数f(x)=sin(ωx+φ)(其中ω>0且|φ|≤$\frac{π}{2}$)的图象如图所示,为了得到y=sinωx的图象,只需把y=f(x)的图象上所有点( )
函数f(x)=sin(ωx+φ)(其中ω>0且|φ|≤$\frac{π}{2}$)的图象如图所示,为了得到y=sinωx的图象,只需把y=f(x)的图象上所有点( )| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向左平移$\frac{π}{3}$个单位长度 |
13.在等差数列{an}中,a1=2,公差为d,则“d=4”是“a1,a2,a5成等比数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
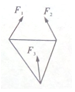 如图,一块均匀的正三角形面的钢板的质量为10$\sqrt{6}$kg,在它的顶点处分别受力F1,F2,F3,每个力同它相邻的三角形的两边之间的角都是60°,且|F1|=|F2|=|F3|.要提起这块钢板,|F1|,|F2|,|F3|均要大于xkg,则x的最小值为$\frac{20\sqrt{2}}{3}$.
如图,一块均匀的正三角形面的钢板的质量为10$\sqrt{6}$kg,在它的顶点处分别受力F1,F2,F3,每个力同它相邻的三角形的两边之间的角都是60°,且|F1|=|F2|=|F3|.要提起这块钢板,|F1|,|F2|,|F3|均要大于xkg,则x的最小值为$\frac{20\sqrt{2}}{3}$.