题目内容
9.在平面直角坐标系xOy中,已知过原点O的动直线l与圆C:x2+y2-6x+5=0相交于不同的两点A,B,若点A恰好使线段OB的中点,则圆心C到直线l的距离为$\frac{3\sqrt{6}}{4}$.分析 化圆的一般式方程为标准方程,设出直线方程,和圆的方程联立,由已知可得A,B两点横坐标的关系,结合根与系数的关系列式求得直线的斜率,得到直线方程,由点到直线的距离公式得答案.
解答 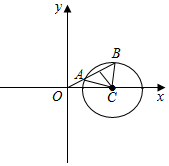 解:由圆C:x2+y2-6x+5=0,得(x-3)2+y2=4,
解:由圆C:x2+y2-6x+5=0,得(x-3)2+y2=4,
画出图形如图,
设OB所在直线方程为y=kx,
联立$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+{y}^{2}-6x+5=0}\end{array}\right.$,得(1+k2)x2-6x+5=0.
设A(x1,y1),B(x2,y2),
则由题意可得:x2=2x1,
∴${x}_{1}+{x}_{2}=3{x}_{1}=\frac{6}{1+{k}^{2}},{x}_{1}{x}_{2}=2{{x}_{1}}^{2}=\frac{5}{1+{k}^{2}}$,
消去x1 得:${k}^{2}=\frac{3}{5}$,∴k=$±\frac{\sqrt{15}}{5}$.
由对称性,不妨取k=$\frac{\sqrt{15}}{5}$,
则直线方程为$y=\frac{\sqrt{15}}{5}x$,即$\sqrt{15}x-5y=0$,
则圆心C(3,0)到直线的距离为d=$\frac{|3\sqrt{15}-5×0|}{\sqrt{15+25}}=\frac{3\sqrt{15}}{2\sqrt{10}}=\frac{3\sqrt{6}}{4}$.
故答案为:$\frac{3\sqrt{6}}{4}$.
点评 本题考查直线与圆的位置关系,考查了一元二次方程根与系数的关系故选的运用,训练了点到直线的距离公式的用法,是中档题.

练习册系列答案
相关题目
19.设Sn是等差数列{an}的前n项和,若a1+a3+a5=3,则S5=( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
17.使arccos(1-x)有意义的x的取值范围是( )
| A. | [1-π,1] | B. | [0,2] | C. | (-∞,1] | D. | [-1,1] |
1.曲线f(x)=ln(2x-1)上的点到直线2x-y+3=0的最短距离是( )
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |