题目内容
13.设数列{an}的前n项和为Sn,已知a1=2,Sn=an+2n-2.(1)求{an}的通项公式;
(2)设bn=log2an.求数列{bn}的前n项和为Tn.
分析 (1)利用递推关系即可得出.
(2)利用等差数列的前n项和公式即可得出.
解答 解:(1)∵Sn=an+2n-2,
∴当n≥2时,an=Sn-Sn-1=(an+2n-2)-$({a}_{n-1}+{2}^{n-1}-2)$,化为an-1=2n-1,因此an=2n,
当n=1时也成立,
∴an=2n.
(2)bn=log2an=n.
∴数列{bn}的前n项和为Tn=$\frac{n(n+1)}{2}$.
点评 本题考查了等差数列的通项公式与前n项和公式、对数运算性质、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知圆C:x2+y2-4x=0,l的方程为mx-3m+y=0,则( )
| A. | l与C相交 | B. | l与C相切 | ||
| C. | l与C相离 | D. | 以上三个选项均有 |
5.函数f(x)满足f($\sqrt{x}$+1)=x+2$\sqrt{x}$,则f(x)的最小值( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
2.设函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-4x+1\\;x≥0}\\{3x+2\\;x<0}\end{array}\right.$若互不相等的实数x1,x2,x3满足f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围是( )
| A. | [$\frac{7}{3}$,+∞) | B. | [$\frac{7}{3}$,4) | C. | ($\frac{7}{3}$,$\frac{11}{3}$] | D. | ($\frac{11}{3}$,+∞) |
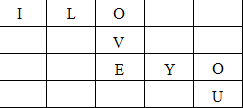 将“I LOVE YOU”8个英文字母填入5×4的方格中,其中“I“字母填入左上角,“U”字母填入右下角,将其余6个英文字母依次填入方格,要求只能横读或竖读成一句原话,如图所示为一种填法,则共有35种不同的填法.(用数字作答)
将“I LOVE YOU”8个英文字母填入5×4的方格中,其中“I“字母填入左上角,“U”字母填入右下角,将其余6个英文字母依次填入方格,要求只能横读或竖读成一句原话,如图所示为一种填法,则共有35种不同的填法.(用数字作答)