题目内容
设函数(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)已知![]() 对任意
对任意![]() 成立,求实数
成立,求实数![]() 的取值范围。
的取值范围。
本题主要考查导数的概念和计算、利用导数研究函数的单调性、利用单调性求最值以及不等式的性质。
解 (1) ![]() 若
若 ![]() 则
则 ![]() 列表如下
列表如下
|
|
|
|
|
| + | 0 | - | - |
| 单调增 | 极大值 | 单调减 | 单调减 |
所以![]() 的单调增区间为
的单调增区间为 ![]() ,单调减区间为
,单调减区间为 ![]() 和
和 ![]() .
.
(2) 在 ![]() 两边取对数, 得
两边取对数, 得 ![]() ,由于
,由于![]() 所以
所以
![]() (1)
(1)
由(1)的结果知,当![]() 时,
时, ![]() ,
,
为使(1)式对所有![]() 成立,当且仅当
成立,当且仅当![]() ,即
,即![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
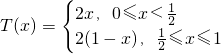
 x))和y=sin(
x))和y=sin( ]时,求y=Tn(x)的解析式;
]时,求y=Tn(x)的解析式;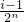 ,
,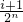 ](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(
](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(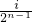 -x)恒成立.
-x)恒成立.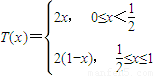
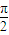 x))和y=sin(
x))和y=sin(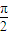 T(x))的解析式;
T(x))的解析式;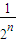 ]时,求y=Tn(x)的解析式;
]时,求y=Tn(x)的解析式;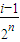 ,
,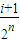 ](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(
](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(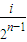 -x)恒成立.
-x)恒成立.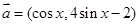 ,
,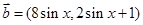 ,
,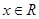 ,设函数
,设函数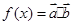 .
.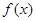 的最大值;
的最大值;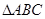 中,角
中,角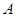 为锐角,角
为锐角,角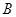 、
、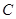 的对边分别为
的对边分别为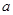 、
、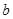 、
、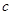 ,
,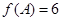 ,且
,且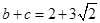 ,求
,求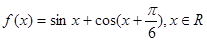 .
.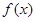 的最小正周期及其在区间
的最小正周期及其在区间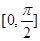 上的值域;
上的值域;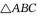 的内角A,B,C的对边分别为
的内角A,B,C的对边分别为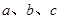 ,若
,若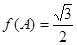 且
且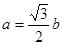 ,求角B的值.
,求角B的值.