题目内容
(2012•泰州二模)若函数f(x)=|2x-1|,则函数g(x)=f[f(x)]+lnx在(0,1)上不同的零点个数为
3
3
.分析:通过x的范围化简函数的表达式,然后转化方程的解为函数的零点,画出函数的图象即可得到函数零点的个数.
解答: 解:∵函数f(x)=|2x-1|,
解:∵函数f(x)=|2x-1|,
所以函数g(x)=
,
g(x)=0,转化为:x∈(0,
),函数y=|4x-1|与y=-lnx;
以及x∈(
,1),函数y=|4x-3|与y=-lnx交点的个数;
函数的图象如图:由图象可知函数的零点为3个.
故答案为:3
 解:∵函数f(x)=|2x-1|,
解:∵函数f(x)=|2x-1|,所以函数g(x)=
|
g(x)=0,转化为:x∈(0,
| 1 |
| 2 |
以及x∈(
| 1 |
| 2 |
函数的图象如图:由图象可知函数的零点为3个.
故答案为:3
点评:本题考查函数的零点个数的判断,函数零点定理的应用,数形结合与分类讨论思想的应用.

练习册系列答案
相关题目
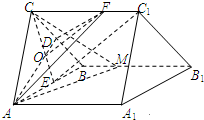 (2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.
(2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.