题目内容
已知sin(α+45°)= ,45°<α<135°,则sinα=
,45°<α<135°,则sinα=
- A.

- B.

- C.

- D.

C
分析:由已知sin(α+45°)= ,45°<α<135°可求cos(α+45°),而α=(α+45°)-45°,利用两角差的正弦公式可求答案.
,45°<α<135°可求cos(α+45°),而α=(α+45°)-45°,利用两角差的正弦公式可求答案.
解答:∵sin(α+45°)= ,45°<α<135°,
,45°<α<135°,
∴cos(α+45°)=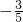
∴sinα=sin[(45°+α)-45°]
=sin(45°+α)cos45°-cos(45+α)sin45°
=
故选C
点评:本题主要考查了求角的函数值,关键是利用了拆角的技巧:α=(45°+α)-45°,常用的拆角有:2α=(α+β)+(α-β);2β=(α+β)-(α-β);α=(α+β)-β;β=(α+β)-α等.
分析:由已知sin(α+45°)=
 ,45°<α<135°可求cos(α+45°),而α=(α+45°)-45°,利用两角差的正弦公式可求答案.
,45°<α<135°可求cos(α+45°),而α=(α+45°)-45°,利用两角差的正弦公式可求答案.解答:∵sin(α+45°)=
 ,45°<α<135°,
,45°<α<135°,∴cos(α+45°)=
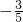
∴sinα=sin[(45°+α)-45°]
=sin(45°+α)cos45°-cos(45+α)sin45°
=

故选C
点评:本题主要考查了求角的函数值,关键是利用了拆角的技巧:α=(45°+α)-45°,常用的拆角有:2α=(α+β)+(α-β);2β=(α+β)-(α-β);α=(α+β)-β;β=(α+β)-α等.

练习册系列答案
相关题目
已知sin(2π-α)=
, α∈(
,2π),则tan(π-α)=( )
| 4 |
| 5 |
| 3π |
| 2 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|