题目内容
若|a|＜1,|b|＜1,求证:
＜1.
思路分析：本题由已知条件不易入手证明,而结论也不易变形,即直接证有困难,因而可联想反证法.
证明:假设≥1,则|a+b|≥|1+ab|,
∴a2+b2+2ab≥1+2ab+a2b2.
∴a2+b2-a2b2-1≥0.
∴a2-1-b2(a2-1)≥0.
∴(a2-1)(1-b2)≥0.
∴
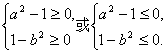
即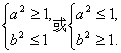
与已知矛盾.
∴
＜1.
练习册系列答案
阅读快车系列答案
相关题目
＜1.阅读快车系列答案题目内容
若|a|＜1,|b|＜1,求证:＜1.
思路分析：本题由已知条件不易入手证明,而结论也不易变形,即直接证有困难,因而可联想反证法.
证明:假设≥1,则|a+b|≥|1+ab|,
∴a2+b2+2ab≥1+2ab+a2b2.
∴a2+b2-a2b2-1≥0.
∴a2-1-b2(a2-1)≥0.
∴(a2-1)(1-b2)≥0.
∴
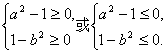
即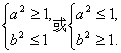与已知矛盾.
∴＜1.
阅读快车系列答案
=a，
1=b，
=c，则
=__________________.
-2
= 
和两个不重合的平面α、β，下列命题中正确命题个数为（ ）
②
④