题目内容
设函数![]() ,且
,且![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)求![]() 与
与![]() 的关系; (2)若
的关系; (2)若![]() 在其定义域内为单调函数,求
在其定义域内为单调函数,求![]() 的取值范围; (3)设
的取值范围; (3)设![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() >
>![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]() (Ⅲ)
(Ⅲ)![]()
解析:
(1)由题意得![]()
![]() 而
而![]() ,所以
,所以![]() 、
、![]() 的关系为
的关系为![]()
(2)由(1)知![]() ,
,
![]() 令
令![]() ,要使
,要使![]() 在其定义域
在其定义域![]() 内是单调函数,只需
内是单调函数,只需![]() 在
在![]() 内满足:
内满足:![]() 恒成立.
恒成立.
①当![]() 时,
时,![]() ,因为
,因为![]() >
>![]() ,所以
,所以![]() <0,
<0,![]() <0,
<0,
∴![]() 在
在![]() 内是单调递减函数,即
内是单调递减函数,即![]() 适合题意;
适合题意;
②当![]() >0时,
>0时,![]() ,其图像为开口向上的抛物线,对称轴为
,其图像为开口向上的抛物线,对称轴为![]() ,
,
∴![]() ,只需
,只需![]() ,即
,即![]() ,
,
∴![]() 在
在![]() 内为单调递增函数, 故
内为单调递增函数, 故![]() 适合题意.
适合题意.
③当![]() <0时,
<0时,![]() ,其图像为开口向下的抛物线,对称轴为
,其图像为开口向下的抛物线,对称轴为![]() ,只要
,只要![]() , 即
, 即![]() 时,
时,![]() 在
在![]() 恒成立,故
恒成立,故![]() <0适合题意.
<0适合题意.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.
(3)∵![]() 在
在![]() 上是减函数,∴
上是减函数,∴![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
即![]() ,
,
①当![]() 时,由(2)知
时,由(2)知![]() 在
在![]() 上递减
上递减![]() <2,不合题意;
<2,不合题意;
②当0<![]() <1时,由
<1时,由![]() ,又由(2)知当
,又由(2)知当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
∴![]() <
<![]() ,不合题意;
,不合题意;
③当![]() 时,由(2)知
时,由(2)知![]() 在
在![]() 上是增函数,
上是增函数,![]() <2,又
<2,又![]() 在
在![]() 上是减函数,
上是减函数,
故只需![]() >
>![]() ,
,![]() , 而
, 而![]() ,
,![]() ,
,
即 ![]() >2,解得
>2,解得![]() >
>![]() ,综上,
,综上,![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
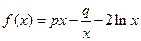 ,且
,且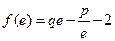 ,其中
,其中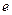 是自然对数的底数.
是自然对数的底数.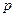 与
与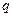 的关系;
的关系;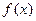 在其定义域内为单调函数,求
在其定义域内为单调函数,求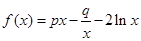 ,且
,且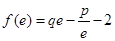 ,其中
,其中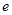 是自然对数的底数.
是自然对数的底数.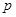 与
与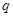 的关系;
的关系;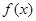 在其定义域内为单调函数,求
在其定义域内为单调函数,求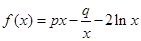 ,且
,且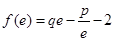 ,其中
,其中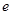 是自然对数的底数.
是自然对数的底数.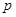 与
与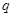 的关系;
的关系;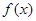 在其定义域内为单调函数,求
在其定义域内为单调函数,求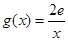 ,若在
,若在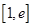 上至少存在一点
上至少存在一点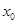 ,使得
,使得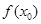 >
>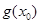 成立,求实数
成立,求实数 ,且
,且 ,其中
,其中 是自然对数的底数.
是自然对数的底数. 与
与 的关系;
的关系; 在其定义域内为单调函数,求
在其定义域内为单调函数,求