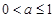题目内容
已知函数 ,下列说法中正确的有 .
,下列说法中正确的有 .(1)f(x)在R上有两个极值点;
(2)f(x)在
 处取得最大值;
处取得最大值;(3)f(x)在
 处取得最小值;
处取得最小值; (4)f(x)在
 处取得极小值
处取得极小值(5)函数f(x)在R上有三个不同的零点.
【答案】分析:依题意,可求得f′(x)=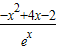 ,利用f′(x)=0可判断(1),利用f(x)=0可判断(5),利用导数判断该函数的单调情况,从而可判断(2)(3)(4).
,利用f′(x)=0可判断(1),利用f(x)=0可判断(5),利用导数判断该函数的单调情况,从而可判断(2)(3)(4).
解答:解:∵f′(x)=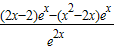 =
=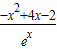 ,
,
∴由f′(x)=0得:x=2-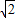 或x=2+
或x=2+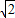 .
.
∴(1)f(x)在R上有两个极值点,正确;
又当x=0或x=2时,f(x)=0,
∴函数f(x)在R上有两个不同的零点,故(5)错误;
由f′(x)>0得2-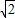 <x<2+
<x<2+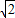 ;
;
由f′(x)<0得x<2-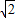 或x>2+
或x>2+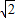 .
.
∴函数f(x)=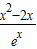 在(-∞,2-
在(-∞,2-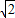 ),(2+
),(2+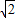 ,+∞)上单调递减,在(2-
,+∞)上单调递减,在(2-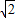 ,2+
,2+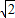 )上单调递增;
)上单调递增;
∴f(x)在x=2-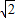 处取得极小值,在x=2+
处取得极小值,在x=2+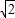 处取得极大值,故(4)错误;
处取得极大值,故(4)错误;
又f(2-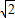 )<0,f(2+
)<0,f(2+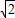 )>0,
)>0,
∴f(x)在x=2-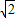 处取得最小值,f(x)在x=2+
处取得最小值,f(x)在x=2+ 取不到最大值,故(3)正确,(2)错误;
取不到最大值,故(3)正确,(2)错误;
综上所述,(1)(3)正确.
故答案为:(1)(3).
点评:本题考查利用导数研究函数的极值,考查根的存在性及根的个数判断,考查分析与运算的能力,属于中档题.
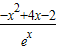 ,利用f′(x)=0可判断(1),利用f(x)=0可判断(5),利用导数判断该函数的单调情况,从而可判断(2)(3)(4).
,利用f′(x)=0可判断(1),利用f(x)=0可判断(5),利用导数判断该函数的单调情况,从而可判断(2)(3)(4).解答:解:∵f′(x)=
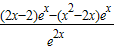 =
=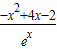 ,
,∴由f′(x)=0得:x=2-
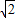 或x=2+
或x=2+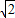 .
.∴(1)f(x)在R上有两个极值点,正确;
又当x=0或x=2时,f(x)=0,
∴函数f(x)在R上有两个不同的零点,故(5)错误;
由f′(x)>0得2-
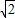 <x<2+
<x<2+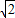 ;
;由f′(x)<0得x<2-
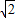 或x>2+
或x>2+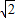 .
.∴函数f(x)=
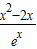 在(-∞,2-
在(-∞,2-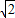 ),(2+
),(2+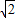 ,+∞)上单调递减,在(2-
,+∞)上单调递减,在(2-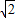 ,2+
,2+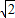 )上单调递增;
)上单调递增;∴f(x)在x=2-
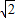 处取得极小值,在x=2+
处取得极小值,在x=2+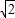 处取得极大值,故(4)错误;
处取得极大值,故(4)错误;又f(2-
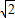 )<0,f(2+
)<0,f(2+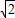 )>0,
)>0,∴f(x)在x=2-
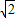 处取得最小值,f(x)在x=2+
处取得最小值,f(x)在x=2+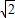 取不到最大值,故(3)正确,(2)错误;
取不到最大值,故(3)正确,(2)错误;综上所述,(1)(3)正确.
故答案为:(1)(3).
点评:本题考查利用导数研究函数的极值,考查根的存在性及根的个数判断,考查分析与运算的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
,则下列说法中正确的是( )
| |x|-a |
| |x-a| |
| A、若a≤0,则f(x)≤1恒成立 |
| B、若f(x)≥1恒成立,则a≥0 |
| C、若a<0,则关于x的方程f(x)=a有解 |
| D、若关于x的方程f(x)=a有解,则0<a≤1 |
 已知函数f(x)=ax3+bx2+cx,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示,则下列说法中不正确的是
已知函数f(x)=ax3+bx2+cx,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示,则下列说法中不正确的是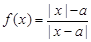 ,则下列说法中正确的是(
)
,则下列说法中正确的是(
)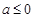 ,则
,则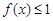 恒成立
恒成立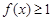 恒成立,则
恒成立,则
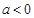 ,则关于
,则关于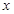 的方程
的方程 有解
有解