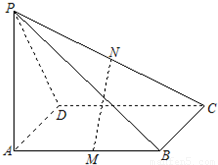
题目内容
如图，PA⊥菱形ABCD所在的平面，M，N分别是AB，PC的中点．
（1）求证：MN∥平面PAD；
（2）求证：平面PBD⊥平面PAC．
（1）求证：MN∥平面PAD；
（2）求证：平面PBD⊥平面PAC．
（1）取CD中点G，连接MG、NG，
∴NG∥PD，MG∥AD，（中位线定理）
∵PD?平面PAD，AD?平面PAD，且PD∩AD=D，
∴平面MNG∥平面PAD，
∵MN?平面MNG，
∴MN∥平面PAD．
（2）因为ABCD是菱形，所以BD⊥AC．
又PA⊥菱形ABCD所在的平面，
所以PA⊥BD，
因为PA∩AC=A，
所以BD⊥面PAC．
又BD?面PBD．
所以平面PBD⊥平面PAC．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
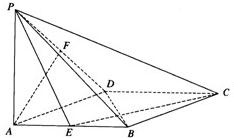如图，在菱形ABCD中，∠DAB=60°，PA⊥底面ABCD，且PA=AB=2，E、F分别是AB与PD的中点．
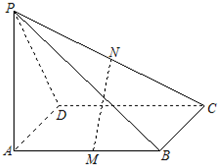如图，PA⊥菱形ABCD所在的平面，M，N分别是AB，PC的中点．
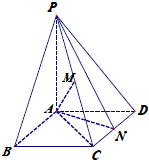如图，在菱形ABCD中，∠BAD=120°，点N为CD中点，PA⊥平面ABCD．