题目内容
6．抛物线y=x2上有一点A的横坐标为a，其中a∈（0，1），过点A的抛物线的切线l交x轴及直线x=1于B，C两点，直线x=1交x轴于D点．（1）求直线l的方程；
（2）求△BCD的面积S（a），并求出a为何值时S（a）有最大值．
分析 （1）利用导数的运算法则可得y′，利用导数的几何意义即可得到切线的斜率，进而得到切线的方程；
（2）利用切线的方程即可得出点B，C的坐标，再利用三角形的面积公式，求得S（a），再由导数求得单调区间和最值，即可得出结论．
解答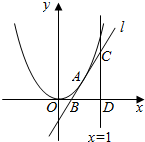 
解：（1）∵y=x2，∴y'=2x，
可得切线l的斜率为2a，
∴切线l的方程是y-a2=2a（x-a），即2ax-y-a2=0；
（2）由2ax-y-a2=0，令y=0，
解得x=$\frac{a}{2}$，∴B（$\frac{a}{2}$，0）；
令x=1，解得y=2a-a2，即C（1，2a-a2），
∴|BD|=1-$\frac{a}{2}$，|CD|=2a-a2，
∴△BCD的面积S（a）=$\frac{1}{2}$（1-$\frac{a}{2}$）（2a-a2）=$\frac{1}{4}$（a3-4a2+4a），
S′（a）=$\frac{1}{4}$（3a2-8a+4）=$\frac{1}{4}$（3a-2）（a-2），
令S'（a）=0，∵a∈（0，1），∴a=$\frac{2}{3}$．
当0＜a＜$\frac{2}{3}$时，S'（a）＞0；
当$\frac{2}{3}$＜a＜1时，S'（a）＜0．
∴a=$\frac{2}{3}$时，S（a）有最大值．
点评 熟练掌握利用导数研究函数的单调性、极值与最值，导数的几何意义等是解题的关键．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
在平面直角坐标系xOy中，对于⊙O：x2+y2=1来说，P是坐标系内任意一点，点P到⊙O的距离SP的定义如下：若P与O重合，SP=r；若P不与O重合，射线OP与⊙O的交点为A，SP=AP的长度（如图）．
11．已知f（x）=x-1，若|f（x）|≥ax-1在x∈R上恒成立，则实数a的取值范围是（ ）
| A． | [0，1] | B． | （-∞，-1]∪[1，+∞） | C． | [-1，1] | D． | （-∞，0]∪[1，+∞） |
18．已知函数f（x）=$\left\{\begin{array}{l}x+2\\{x^2}\\ 2x\end{array}$$\begin{array}{l}（x≤-1），\\（-1＜x＜2），\\（x≥2），\end{array}$如果f（x）=3，那么x的值是（ ）
| A． | 1 | B． | $\sqrt{3}$ | C． | $±\sqrt{3}$ | D． | $\frac{3}{2}$ |