题目内容
设函数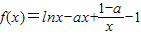 .
.(Ⅰ)当a=1时,过原点的直线与函数f(x)的图象相切于点P,求点P的坐标;
(Ⅱ)当
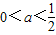 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;(Ⅲ)当
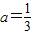 时,设函数
时,设函数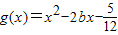 ,若对于?x1∈(0,e],?x2∈[0,1]使f(x1)≥g(x2)成立,求实数b的取值范围.(e是自然对数的底,
,若对于?x1∈(0,e],?x2∈[0,1]使f(x1)≥g(x2)成立,求实数b的取值范围.(e是自然对数的底,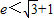 )
)
【答案】分析:(Ⅰ)确定函数f(x)的定义域,求出导函数,利用过原点的直线与函数f(x)的图象相切于点P,可求点P的坐标;
(Ⅱ)求导函数,f'(x)<0,可得函数的单调减区间;f'(x)>0,可得出函数f(x)的单调递增区间;
(Ⅲ)?x1∈(0,e],?x2∈[0,1]使f(x1)≥g(x2)成立,等价于g(x)在[0,1]上的最小值不大于f(x)在(0,e]上的最小值,由此可求b的取值范围.
解答:解:函数f(x)的定义域为(0,+∞),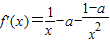 (2分)
(2分)
(Ⅰ)设点P(x,y)(x>0),当a=1时,f(x)=lnx-x-1,则y=lnx-x-1,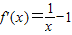 ,
,
∴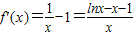 (3分)
(3分)
解得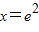 ,故点P 的坐标为(e2,1-e2)(4分)
,故点P 的坐标为(e2,1-e2)(4分)
(Ⅱ)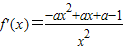 =
=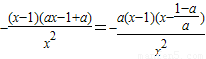
∵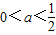 ,∴
,∴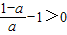 (5分)
(5分)
∴当0<x<1,或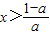 时,f'(x)<0;当
时,f'(x)<0;当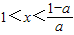 时,f'(x)>0
时,f'(x)>0
故当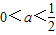 时,函数f(x)的单调递增区间为
时,函数f(x)的单调递增区间为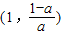 ;
;
单调递减区间为(0,1),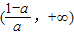 (7分)
(7分)
(Ⅲ)当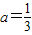 时,
时,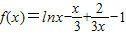
由(Ⅱ)可知函数f(x)在(0,1)上是减函数,在(1,2)上为增函数,在(2,e]上为减函数,且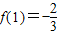 ,
,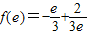
∵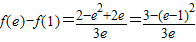 ,又
,又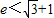 ,∴(e-1)2<3,
,∴(e-1)2<3,
∴f(e)>f(1),故函数f(x)在(0,e]上的最小值为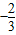 (9分)
(9分)
若?x1∈(0,e],?x2∈[0,1]使f(x1)≥g(x2)成立,等价于g(x)在[0,1]上的最小值不大于f(x)在(0,e]上的最小值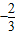 (*) (10分)
(*) (10分)
又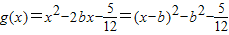 ,x∈[0,1]
,x∈[0,1]
①当b<0时,g(x)在[0,1]上为增函数,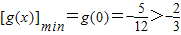 与(*)矛盾
与(*)矛盾
②当0≤b≤1时,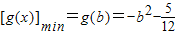 ,由
,由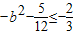 及0≤b≤1得,
及0≤b≤1得,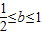
③当b>1时,g(x)在[0,1]上为减函数,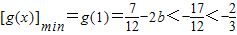 ,
,
此时b>1
综上,b的取值范围是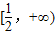 (12分)
(12分)
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查函数的最值,解题的关键是将?x1∈(0,e],?x2∈[0,1]使f(x1)≥g(x2)成立,转化为g(x)在[0,1]上的最小值不大于f(x)在(0,e]上的最小值
(Ⅱ)求导函数,f'(x)<0,可得函数的单调减区间;f'(x)>0,可得出函数f(x)的单调递增区间;
(Ⅲ)?x1∈(0,e],?x2∈[0,1]使f(x1)≥g(x2)成立,等价于g(x)在[0,1]上的最小值不大于f(x)在(0,e]上的最小值,由此可求b的取值范围.
解答:解:函数f(x)的定义域为(0,+∞),
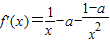 (2分)
(2分)(Ⅰ)设点P(x,y)(x>0),当a=1时,f(x)=lnx-x-1,则y=lnx-x-1,
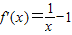 ,
,∴
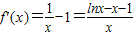 (3分)
(3分)解得
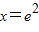 ,故点P 的坐标为(e2,1-e2)(4分)
,故点P 的坐标为(e2,1-e2)(4分)(Ⅱ)
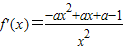 =
=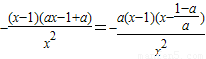
∵
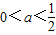 ,∴
,∴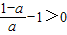 (5分)
(5分)∴当0<x<1,或
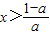 时,f'(x)<0;当
时,f'(x)<0;当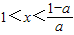 时,f'(x)>0
时,f'(x)>0故当
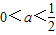 时,函数f(x)的单调递增区间为
时,函数f(x)的单调递增区间为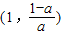 ;
;单调递减区间为(0,1),
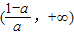 (7分)
(7分)(Ⅲ)当
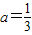 时,
时,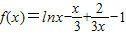
由(Ⅱ)可知函数f(x)在(0,1)上是减函数,在(1,2)上为增函数,在(2,e]上为减函数,且
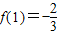 ,
,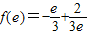
∵
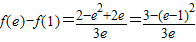 ,又
,又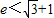 ,∴(e-1)2<3,
,∴(e-1)2<3,∴f(e)>f(1),故函数f(x)在(0,e]上的最小值为
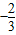 (9分)
(9分)若?x1∈(0,e],?x2∈[0,1]使f(x1)≥g(x2)成立,等价于g(x)在[0,1]上的最小值不大于f(x)在(0,e]上的最小值
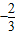 (*) (10分)
(*) (10分)又
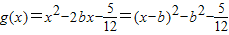 ,x∈[0,1]
,x∈[0,1]①当b<0时,g(x)在[0,1]上为增函数,
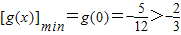 与(*)矛盾
与(*)矛盾②当0≤b≤1时,
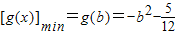 ,由
,由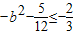 及0≤b≤1得,
及0≤b≤1得,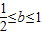
③当b>1时,g(x)在[0,1]上为减函数,
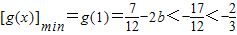 ,
,此时b>1
综上,b的取值范围是
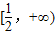 (12分)
(12分)点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查函数的最值,解题的关键是将?x1∈(0,e],?x2∈[0,1]使f(x1)≥g(x2)成立,转化为g(x)在[0,1]上的最小值不大于f(x)在(0,e]上的最小值

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 。
。 的极值;
的极值; 2时,讨论函数
2时,讨论函数 成立,求
成立,求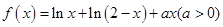 。
。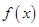 的单调区间。
的单调区间。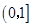 上的最大值为
上的最大值为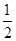 ,求a的值。
,求a的值。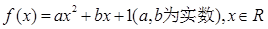 ,设函数
,设函数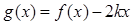 ,
,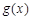 在
在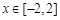 上的最小值
上的最小值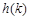 .
.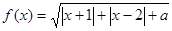 。
。 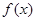 的定义域。
的定义域。