题目内容
若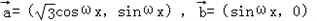 ,其中ω>0,函数
,其中ω>0,函数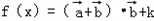 .(1)若f(x)图象申相邻两条对称轴间的距离不小于
.(1)若f(x)图象申相邻两条对称轴间的距离不小于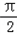 ,求ω的取值范围.
,求ω的取值范围.
(2)若f(x)的最小正周期为π,且当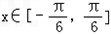 时,f(x)的最大值是
时,f(x)的最大值是 ,求f(x)的解析式.
,求f(x)的解析式.
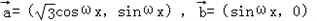 ,其中ω>0,函数
,其中ω>0,函数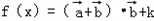 .(1)若f(x)图象申相邻两条对称轴间的距离不小于
.(1)若f(x)图象申相邻两条对称轴间的距离不小于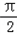 ,求ω的取值范围.
,求ω的取值范围.(2)若f(x)的最小正周期为π,且当
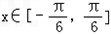 时,f(x)的最大值是
时,f(x)的最大值是 ,求f(x)的解析式.
,求f(x)的解析式.解:(1)∵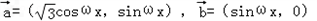 ,
,
∴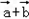 =(
=(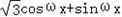 ,sin?x),
,sin?x),
∴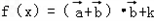
=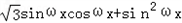 +k
+k
=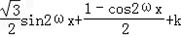
=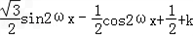
=sin(2?x﹣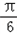 )+k+
)+k+ .
.
∵f(x)图象中相邻两条对称轴间的距离不小于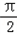 ,
,
∴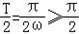 ,∴ω≤1,
,∴ω≤1,
∵ω>0,∴0<ω≤1.
(2)∵T=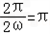 ,∴ω=1,
,∴ω=1,
∴f(x)=sin(2x﹣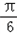 )+k+
)+k+ ,
,
∵x∈[﹣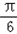 ,
,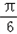 ],
],
∴2x﹣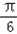 ?[﹣
?[﹣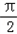 ,
,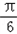 ],
],
从而当2x﹣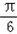 =
=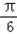 ,即x=
,即x=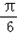 时,
时,
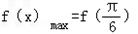 =sin
=sin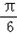 +k+
+k+ =k+1=
=k+1= ,
,
∴k=﹣ ,
,
故f(x)=sin(2x﹣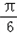 ).
).
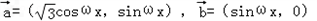 ,
,∴
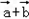 =(
=(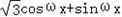 ,sin?x),
,sin?x),∴
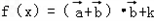
=
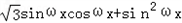 +k
+k=
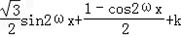
=
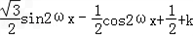
=sin(2?x﹣
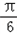 )+k+
)+k+ .
.∵f(x)图象中相邻两条对称轴间的距离不小于
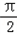 ,
,∴
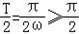 ,∴ω≤1,
,∴ω≤1,∵ω>0,∴0<ω≤1.
(2)∵T=
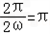 ,∴ω=1,
,∴ω=1,∴f(x)=sin(2x﹣
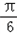 )+k+
)+k+ ,
,∵x∈[﹣
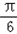 ,
,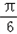 ],
],∴2x﹣
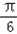 ?[﹣
?[﹣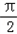 ,
,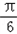 ],
],从而当2x﹣
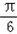 =
=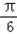 ,即x=
,即x=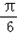 时,
时,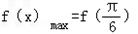 =sin
=sin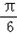 +k+
+k+ =k+1=
=k+1= ,
,∴k=﹣
 ,
,故f(x)=sin(2x﹣
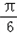 ).
).
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目