Question

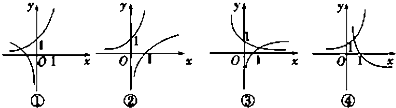
函数f（x）=a^x与g（x）=ax-a的图象有可能是图中的

1. A.
   
2. B.
   
3. C.
   
4. D.
   

Answer 1

D
分析：分别讨论参数a的各种取值与对应图象的关系．A中0＜a＜1，B中a＞1，C中0＜a＜1，D中＞1．
解答：A由指数函数的图象可知，0＜a＜1．此时直线g（x）=ax-a的斜率应为正，所以A错误．
B．由指数函数的图象可知，a＞1．此时直线g（x）=ax-a的斜率应为正，纵截距为-a＜0，所以B错误．
C．由指数函数的图象可知，0＜a＜1．此时直线g（x）=ax-a的斜率应为正，且斜率0＜k＜1．而C中直线的斜率k＞1，所以C错误．
D．由指数函数的图象可知，a＞1．．此时直线g（x）=ax-a的斜率应为正，纵截距为-a＜0，所以D有可能．
故选D．
点评：本题考查指数函数的图象与性质，以及直线的斜率与截距问题．在判断过程中应先确定一个图象中a的取值范围，然后在比较一下另一个图象是否对应．