题目内容
设函数
，（ω＞0），x∈（-∞，+∞），且以
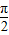为最小正周期．（1）求f（0）；
（2）求f（x）的解析式；
（3）已知
，求sinαtanα的值．
【答案】分析：（1）代入已知关系式即可求得f（0）；
（2）利用正弦函数的周期公式即可求得ω，从而可得f（x）的解析式；
（3）由由f（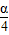
+
）=
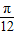，可求得cosα的值，从而可求得sinαtanα的值．
解答：解：（1）由题设可知f（0）=3sin（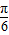
）=
---------（2分）
（2）∵f（x）的最小正周期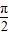
，
∴ω=
=4----------（5分）
∴f（x）=3sin（4x+
）-------------（6分）
（3）由f（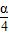
+
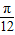）=3sin（α+
+
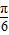）=3cosα=
，…（9分）
∴cosα=
，sin2α=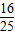
，
∴sinαtanα=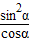
=
=
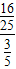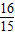…（12分）
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查三角函数的恒等变换及化简求值，属于中档题．
（2）利用正弦函数的周期公式即可求得ω，从而可得f（x）的解析式；
（3）由由f（
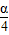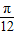+）=，可求得cosα的值，从而可求得sinαtanα的值．解答：解：（1）由题设可知f（0）=3sin（
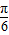）=---------（2分）（2）∵f（x）的最小正周期
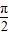，∴ω=
=4----------（5分）∴f（x）=3sin（4x+
）-------------（6分）（3）由f（
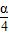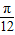+）=3sin（α++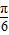）=3cosα=，…（9分）∴cosα=
，sin2α=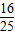，∴sinαtanα=
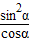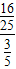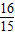==…（12分）点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查三角函数的恒等变换及化简求值，属于中档题．
练习册系列答案
相关题目
设函数f(x)=
(0≤x＜1)的反函数为f-1（x），则（ ）
| 1 | ||
1-
|
| A、f-1（x）在其定义域上是增函数且最大值为1 |
| B、f-1（x）在其定义域上是减函数且最小值为0 |
| C、f-1（x）在其定义域上是减函数且最大值为1 |
| D、f-1（x）在其定义域上是增函数且最小值为0 |